2594. Minimum Time to Repair Cars

2594. Minimum Time to Repair Cars Difficulty: Medium Topics: Array, Binary Search You are given an integer array ranks representing the ranks of some mechanics. ranksi is the rank of the ith mechanic. A mechanic with a rank r can repair n cars in r * n2 minutes. You are also given an integer cars representing the total number of cars waiting in the garage to be repaired. Return the minimum time taken to repair all the cars. Note: All the mechanics can repair the cars simultaneously. Example 1: Input: ranks = [4,2,3,1], cars = 10 Output: 16 Explanation: The first mechanic will repair two cars. The time required is 4 * 2 * 2 = 16 minutes. The second mechanic will repair two cars. The time required is 2 * 2 * 2 = 8 minutes. The third mechanic will repair two cars. The time required is 3 * 2 * 2 = 12 minutes. The fourth mechanic will repair four cars. The time required is 1 * 4 * 4 = 16 minutes. It can be proved that the cars cannot be repaired in less than 16 minutes. Example 2: Input: ranks = [5,1,8], cars = 6 Output: 16 Explanation: The first mechanic will repair one car. The time required is 5 * 1 * 1 = 5 minutes. The second mechanic will repair four cars. The time required is 1 * 4 * 4 = 16 minutes. The third mechanic will repair one car. The time required is 8 * 1 * 1 = 8 minutes. It can be proved that the cars cannot be repaired in less than 16 minutes. Constraints: 1 Explanation: Binary Search Setup: We initialize low to 1 and high to the maximum possible time, which is when the highest-ranked mechanic repairs all cars alone. Binary Search Loop: In each iteration, we calculate the midpoint mid and check if all cars can be repaired within mid minutes. Feasibility Check: For each mechanic's rank, we compute the maximum number of cars they can repair in mid minutes. Summing these values gives the total number of cars that can be repaired. If this sum meets or exceeds the required number of cars, mid is a feasible time, and we adjust the search range to find a smaller feasible time. Otherwise, we increase the search range. Termination: The loop terminates when low equals high, which is the minimum feasible time. This approach efficiently narrows down the possible minimum time using binary search, ensuring an optimal solution with a time complexity of O(n log(max_rank * cars^2)), where n is the number of mechanics. Contact Links If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks

Mar 16, 2025 - 17:58

Difficulty: Medium

Topics: Array, Binary Search

You are given an integer array ranks representing the ranks of some mechanics. ranksi is the rank of the i^th mechanic. A mechanic with a rank r can repair n cars in r * n² minutes.

You are also given an integer cars representing the total number of cars waiting in the garage to be repaired.

Return the minimum time taken to repair all the cars.

Note: All the mechanics can repair the cars simultaneously.

Example 1:

Input: ranks = [4,2,3,1], cars = 10
Output: 16
Explanation:
- The first mechanic will repair two cars. The time required is 4 * 2 * 2 = 16 minutes.
- The second mechanic will repair two cars. The time required is 2 * 2 * 2 = 8 minutes.
- The third mechanic will repair two cars. The time required is 3 * 2 * 2 = 12 minutes.
- The fourth mechanic will repair four cars. The time required is 1 * 4 * 4 = 16 minutes.
- It can be proved that the cars cannot be repaired in less than 16 minutes.

Example 2:

Input: ranks = [5,1,8], cars = 6
Output: 16
Explanation:
- The first mechanic will repair one car. The time required is 5 * 1 * 1 = 5 minutes.
- The second mechanic will repair four cars. The time required is 1 * 4 * 4 = 16 minutes.
- The third mechanic will repair one car. The time required is 8 * 1 * 1 = 8 minutes.
- It can be proved that the cars cannot be repaired in less than 16 minutes.

Constraints:

1 <= ranks.length <= 10⁵
1 <= ranks[i] <= 100
1 <= cars <= 10⁶

Hint:

For a predefined fixed time, can all the cars be repaired?
Try using binary search on the answer.

Solution:

We need to determine the minimum time required for a group of mechanics with different ranks to repair all the cars in a garage. Each mechanic's repair time is determined by their rank and the number of cars they repair. The goal is to minimize the maximum time taken by any mechanic.

Approach

The problem can be efficiently solved using binary search on the possible time values. The key insight is to check if a given time T allows all cars to be repaired by the mechanics working simultaneously. For each mechanic with rank r, the maximum number of cars they can repair in time T is given by floor(sqrt(T / r)). We sum these values for all mechanics and check if the total is at least the number of cars needing repair. If it is, T is a feasible time, and we search for a smaller time; otherwise, we search for a larger time.

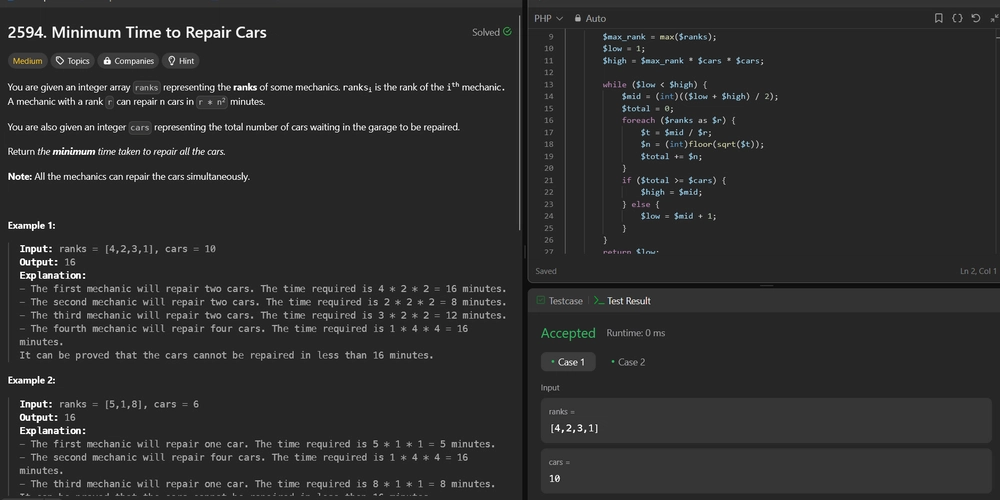
Let's implement this solution in PHP: 2594. Minimum Time to Repair Cars


/**
 * @param Integer[] $ranks
 * @param Integer $cars
 * @return Integer
 */
function repairCars($ranks, $cars) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example Usage:
$ranks1 = [4, 2, 3, 1];
$cars1 = 10;
echo repairCars($ranks1, $cars1) . "\n"; // Output: 16

$ranks2 = [5, 1, 8];
$cars2 = 6;
echo repairCars($ranks2, $cars2) . "\n"; // Output: 16
?>

Explanation:

Binary Search Setup: We initialize low to 1 and high to the maximum possible time, which is when the highest-ranked mechanic repairs all cars alone.
Binary Search Loop: In each iteration, we calculate the midpoint mid and check if all cars can be repaired within mid minutes.
Feasibility Check: For each mechanic's rank, we compute the maximum number of cars they can repair in mid minutes. Summing these values gives the total number of cars that can be repaired. If this sum meets or exceeds the required number of cars, mid is a feasible time, and we adjust the search range to find a smaller feasible time. Otherwise, we increase the search range.
Termination: The loop terminates when low equals high, which is the minimum feasible time.

This approach efficiently narrows down the possible minimum time using binary search, ensuring an optimal solution with a time complexity of O(n log(max_rank * cars^2)), where n is the number of mechanics.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks