Sieve of Eratosthenes: What is it? And how to implement sieve in C++
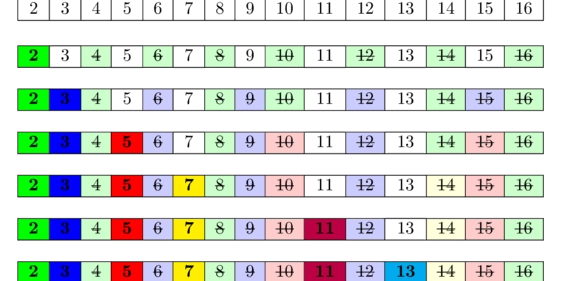
What is Sieve of Eratosthenes Sive of Eratosthenes is one an ancient algorithm that finds all prime numbers in a given range. It is also used for finding all divisors of a number with a faster time complexity. Sieve Algorithm The algorithm starts by generating a boolean array Boolarray to store whether i is a prime number or not. 2. Every number in the array is set to be TRUE by default. 3. The outer loop of the algorithm iterates Boolarray from 2 to sqrt(n) . - Inner loop iterates through j and accumulate by i(for all multiples of i), all multiples are marked FALSE(since these are not prime numbers). - Inner loop works by marking FALSE on all multiples of i We are left with b with all prime numbers being TRUE in the range of 1 to n. Time Complexity The time complexity of the above logic is O(n log log n). The outer loop runs for sqrt(n), while the inner loop runs roughly n / i times. Example in C++ #include using namespace std; int main(){ int n; cin>>n; bool Boolarray[n+1]; for(int i = 2; i
What is Sieve of Eratosthenes
Sive of Eratosthenes is one an ancient algorithm that finds all prime numbers in a given range. It is also used for finding all divisors of a number with a faster time complexity.
Sieve Algorithm
- The algorithm starts by generating a boolean array
Boolarrayto store whetheriis a prime number or not. 2. Every number in the array is set to be TRUE by default. 3. The outer loop of the algorithm iterates Boolarray from 2 tosqrt(n). - Inner loop iterates through j and accumulate by i(for all multiples of i), all multiples are marked FALSE(since these are not prime numbers). - Inner loop works by marking FALSE on all multiples ofi
- We are left with
bwith all prime numbers being TRUE in the range of 1 to n.
Time Complexity
The time complexity of the above logic is O(n log log n). The outer loop runs for sqrt(n), while the inner loop runs roughly n / i times.
Example in C++
#includeImage Source https://cp-algorithms.com/algebra/sieve-of-eratosthenes.html






































































































































































![[The AI Show Episode 142]: ChatGPT’s New Image Generator, Studio Ghibli Craze and Backlash, Gemini 2.5, OpenAI Academy, 4o Updates, Vibe Marketing & xAI Acquires X](https://www.marketingaiinstitute.com/hubfs/ep%20142%20cover.png)






















































































































![[FREE EBOOKS] The Kubernetes Bible, The Ultimate Linux Shell Scripting Guide & Four More Best Selling Titles](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)



![From drop-out to software architect with Jason Lengstorf [Podcast #167]](https://cdn.hashnode.com/res/hashnode/image/upload/v1743796461357/f3d19cd7-e6f5-4d7c-8bfc-eb974bc8da68.png?#)




































































































.png?#)




.jpg?#)


















 (1).webp?#)












_Christophe_Coat_Alamy.jpg?#)


































































































![Rapidus in Talks With Apple as It Accelerates Toward 2nm Chip Production [Report]](https://www.iclarified.com/images/news/96937/96937/96937-640.jpg)