RLVR Doesn't Expand LLM Reasoning, Just Optimizes Sampling: New Study

This is a Plain English Papers summary of a research paper called RLVR Doesn't Expand LLM Reasoning, Just Optimizes Sampling: New Study. If you like these kinds of analysis, you should join AImodels.fyi or follow us on Twitter. Challenging the Self-Improvement Narrative of RLVR in LLMs Reinforcement Learning with Verifiable Rewards (RLVR) has recently driven significant advancements in reasoning-centric large language models (LLMs) like OpenAI-o1, DeepSeek-R1, and Kimi-1.5. These models have demonstrated remarkable capabilities in complex logical tasks involving mathematics and programming. Unlike traditional instruction-tuned approaches that rely on human-curated annotations, RLVR starts with a pretrained base model and optimizes it via reinforcement learning using automatically computable rewards. These rewards come from simple verification methods: matching ground-truth solutions in mathematics or passing unit tests in code. The conventional belief holds that RLVR enables models to autonomously develop advanced reasoning behaviors beyond their base models' capabilities. This self-improvement perspective positions RLVR as a pathway toward continuously evolving artificial intelligence with expanding reasoning capabilities. But does RLVR truly enable new reasoning capabilities? Or is something else happening beneath the surface? This research critically examines this assumption using the pass@k metric with large values of k to explore reasoning capability boundaries across diverse model families and benchmarks. This methodology allows for rigorous testing of whether RLVR truly enables models to solve problems beyond their base models' capabilities. The surprising findings challenge conventional understanding: RLVR does not elicit fundamentally new reasoning patterns. While RL-trained models outperform base models when generating single answers (k=1), base models achieve comparable or even higher success rates when allowed multiple attempts (large k values). This suggests that training language models to reason efficiently through RLVR may not be expanding their fundamental capabilities, but rather optimizing their sampling behavior. Understanding How to Measure Reasoning Capabilities in LLMs The Mechanics of Reinforcement Learning with Verifiable Rewards RLVR starts with an LLM that generates token sequences based on prompts. A deterministic verifier provides binary rewards based on correctness - a reward of 1 if the model's final answer matches the ground truth, and 0 otherwise. Format rewards may also be added to encourage proper separation of reasoning and answers. The goal of RLVR is to maximize the expected reward across all prompts. Popular implementation algorithms include: Proximal Policy Optimization (PPO): Uses a clipped surrogate objective with advantages estimated by a value network GRPO: A critic-free variant that normalizes rewards within groups of responses RLOO: Adopts a leave-one-out baseline within each training batch These policy gradient methods aim to increase the probability of rewarded responses while decreasing the probability of unrewarded ones, gradually steering the model toward more successful reasoning paths. Establishing Metrics for Reasoning Capacity Boundaries Traditional evaluation methods like single-pass success rates or nucleus sampling reflect average-case performance rather than a model's true reasoning potential. These approaches may underestimate capabilities when models fail after only a few attempts at difficult problems, even if they could succeed with more sampling. To properly evaluate reasoning boundaries, this research employs the pass@k metric, which considers a problem solved if any of k samples yields a correct answer. This approach reveals whether a model has the fundamental capacity to solve a problem, even if the solution isn't efficiently sampled. The unbiased estimator for pass@k is calculated as: pass@k := E[1 - (n-c choose k)/(n choose k)] Where c is the number of correct samples out of n attempts. For math problems, where "lucky guesses" can occur, the researchers filtered out easily hackable problems and manually verified the correctness of reasoning chains. This rigorous approach ensures an accurate assessment of true reasoning capabilities rather than coincidental correct answers. Table showing the experimental setup across different tasks (mathematics, code generation, visual reasoning), using various model families, RL frameworks, algorithms, and benchmarks. Examining RLVR's Effects Across Different Reasoning Tasks The research evaluates RLVR's impact across three representative domains: mathematics, code generation, and visual reasoning. All experiments maintain consistent sampling parameters: temperature of 0.6, top-p value of 0.95, and maximum generation of 16,384 tokens. To ensure fairness, the evaluation avoids few-shot prompts for base models, eliminating po

Apr 26, 2025 - 16:58

This is a Plain English Papers summary of a research paper called RLVR Doesn't Expand LLM Reasoning, Just Optimizes Sampling: New Study. If you like these kinds of analysis, you should join AImodels.fyi or follow us on Twitter.

Challenging the Self-Improvement Narrative of RLVR in LLMs

Reinforcement Learning with Verifiable Rewards (RLVR) has recently driven significant advancements in reasoning-centric large language models (LLMs) like OpenAI-o1, DeepSeek-R1, and Kimi-1.5. These models have demonstrated remarkable capabilities in complex logical tasks involving mathematics and programming.

Unlike traditional instruction-tuned approaches that rely on human-curated annotations, RLVR starts with a pretrained base model and optimizes it via reinforcement learning using automatically computable rewards. These rewards come from simple verification methods: matching ground-truth solutions in mathematics or passing unit tests in code.

The conventional belief holds that RLVR enables models to autonomously develop advanced reasoning behaviors beyond their base models' capabilities. This self-improvement perspective positions RLVR as a pathway toward continuously evolving artificial intelligence with expanding reasoning capabilities.

But does RLVR truly enable new reasoning capabilities? Or is something else happening beneath the surface?

This research critically examines this assumption using the pass@k metric with large values of k to explore reasoning capability boundaries across diverse model families and benchmarks. This methodology allows for rigorous testing of whether RLVR truly enables models to solve problems beyond their base models' capabilities.

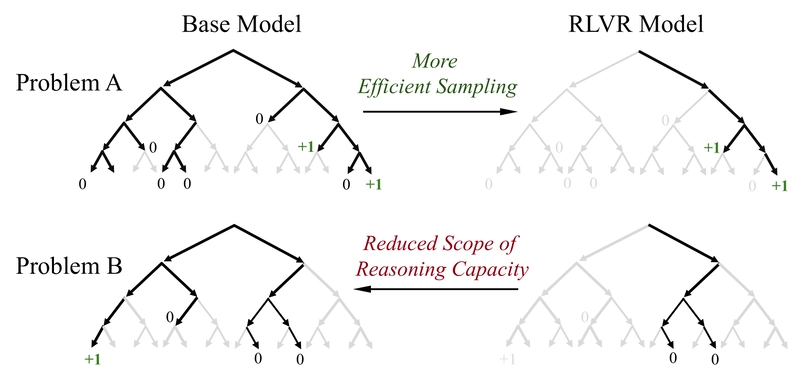
The surprising findings challenge conventional understanding: RLVR does not elicit fundamentally new reasoning patterns. While RL-trained models outperform base models when generating single answers (k=1), base models achieve comparable or even higher success rates when allowed multiple attempts (large k values). This suggests that training language models to reason efficiently through RLVR may not be expanding their fundamental capabilities, but rather optimizing their sampling behavior.

Understanding How to Measure Reasoning Capabilities in LLMs

The Mechanics of Reinforcement Learning with Verifiable Rewards

RLVR starts with an LLM that generates token sequences based on prompts. A deterministic verifier provides binary rewards based on correctness - a reward of 1 if the model's final answer matches the ground truth, and 0 otherwise. Format rewards may also be added to encourage proper separation of reasoning and answers.

The goal of RLVR is to maximize the expected reward across all prompts. Popular implementation algorithms include:

Proximal Policy Optimization (PPO): Uses a clipped surrogate objective with advantages estimated by a value network
GRPO: A critic-free variant that normalizes rewards within groups of responses
RLOO: Adopts a leave-one-out baseline within each training batch

These policy gradient methods aim to increase the probability of rewarded responses while decreasing the probability of unrewarded ones, gradually steering the model toward more successful reasoning paths.

Establishing Metrics for Reasoning Capacity Boundaries

Traditional evaluation methods like single-pass success rates or nucleus sampling reflect average-case performance rather than a model's true reasoning potential. These approaches may underestimate capabilities when models fail after only a few attempts at difficult problems, even if they could succeed with more sampling.

To properly evaluate reasoning boundaries, this research employs the pass@k metric, which considers a problem solved if any of k samples yields a correct answer. This approach reveals whether a model has the fundamental capacity to solve a problem, even if the solution isn't efficiently sampled.

The unbiased estimator for pass@k is calculated as:

pass@k := E[1 - (n-c choose k)/(n choose k)]

Where c is the number of correct samples out of n attempts.

For math problems, where "lucky guesses" can occur, the researchers filtered out easily hackable problems and manually verified the correctness of reasoning chains. This rigorous approach ensures an accurate assessment of true reasoning capabilities rather than coincidental correct answers.

Table showing the experimental setup across different tasks (mathematics, code generation, visual reasoning), using various model families, RL frameworks, algorithms, and benchmarks.

Examining RLVR's Effects Across Different Reasoning Tasks

The research evaluates RLVR's impact across three representative domains: mathematics, code generation, and visual reasoning. All experiments maintain consistent sampling parameters: temperature of 0.6, top-p value of 0.95, and maximum generation of 16,384 tokens.

To ensure fairness, the evaluation avoids few-shot prompts for base models, eliminating potential confounding effects from in-context examples. Both base and RLVR models receive identical zero-shot prompts or benchmark-provided defaults.

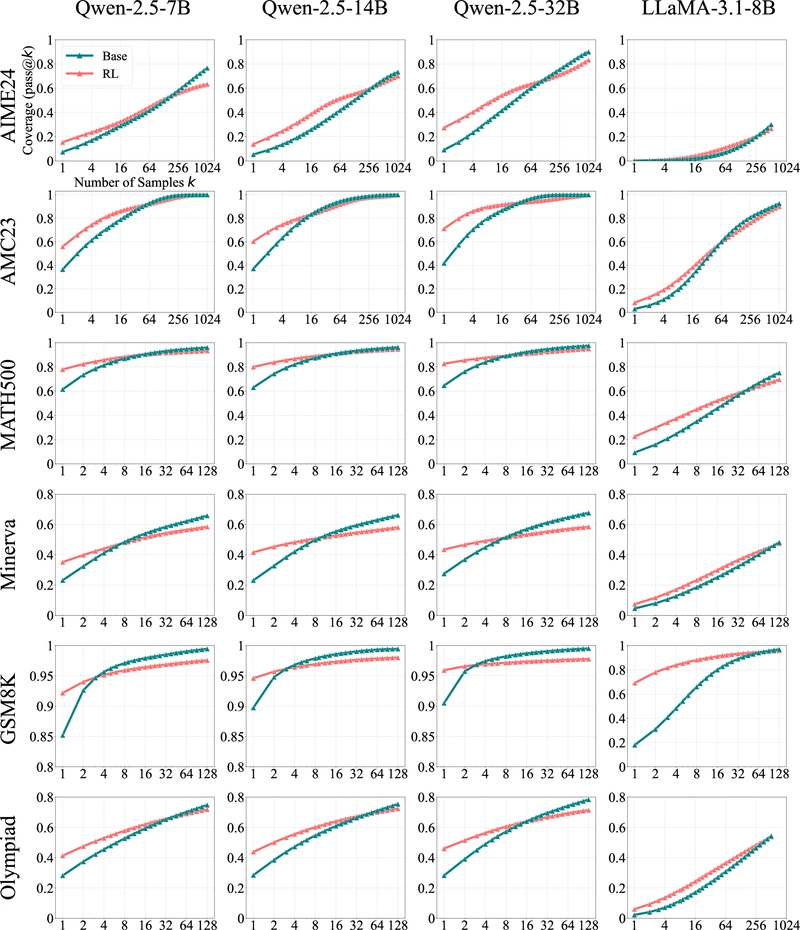
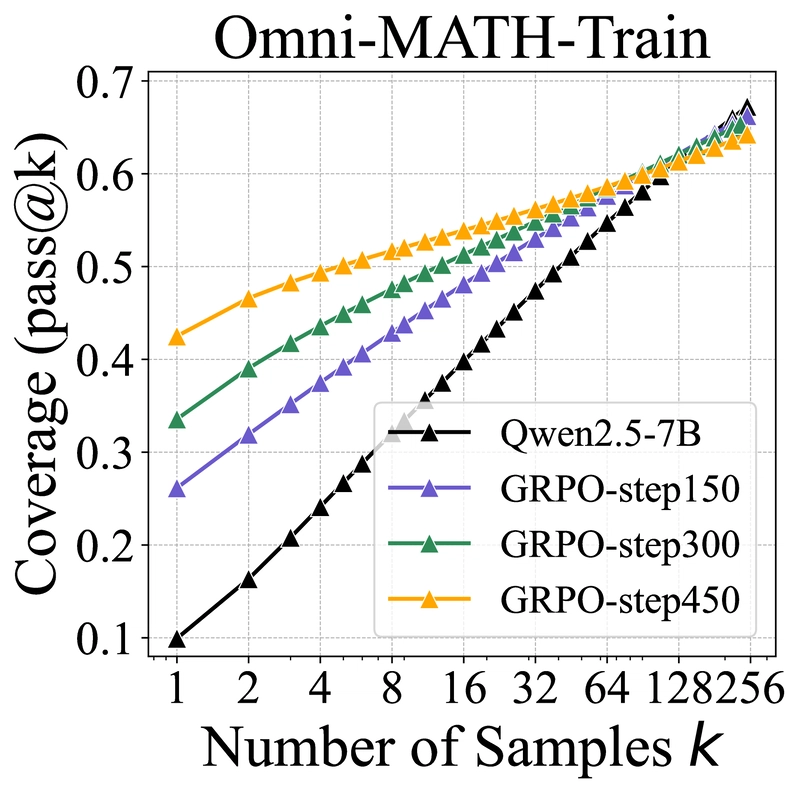
Mathematical Reasoning: Efficiency Gains at the Cost of Coverage

The mathematical reasoning evaluation used multiple LLM families (Qwen-2.5 in 7B/14B/32B sizes and LLaMA-3.1-8B) on benchmarks with varying difficulty levels, including GSM8K, MATH500, Minerva, Olympiad, AIME24, and AMC23.

The results reveal a consistent pattern: at low k values (e.g., k=1), RL-trained models significantly outperform their base counterparts. However, as k increases, base models show steeper improvement curves and eventually surpass the RL models. For example, on the Minerva benchmark with a 32B model, the base model outperforms the RL model by approximately 9% at k=128.

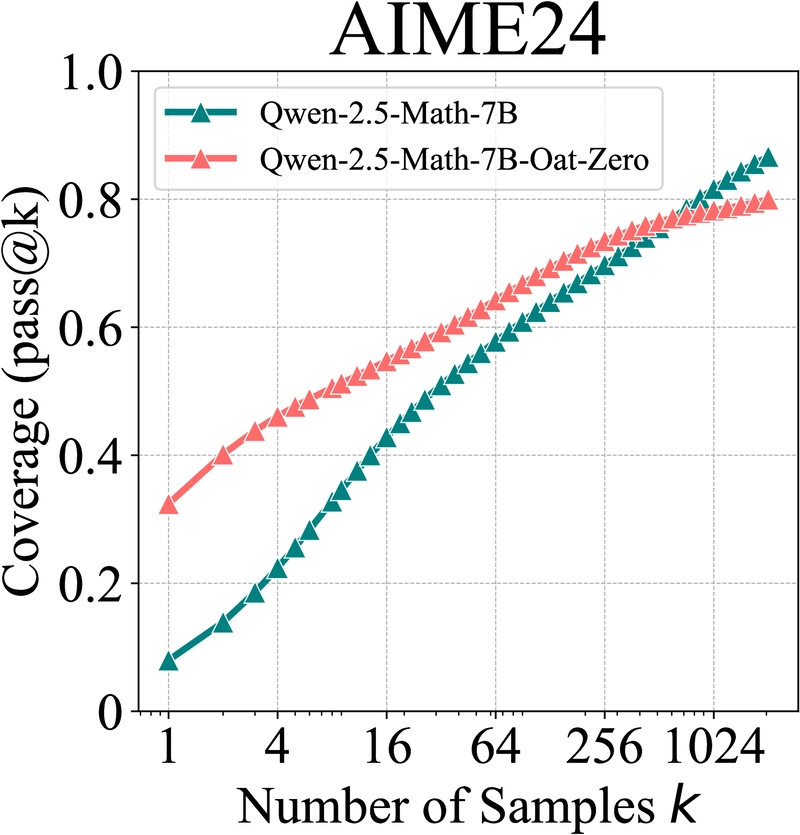
Graph showing how Oat-Zero performs on AIME24 compared to the base model, with similar crossover behavior at large k values.

Even for Oat-Zero, which shows nearly 30% higher performance than its base model at k=1 on the challenging AIME24 benchmark, the base model eventually surpasses it with sufficient sampling.

To validate these findings, the researchers manually inspected chains of thought for the most challenging solvable problems. The results confirmed that even on extremely difficult questions, correct answers predominantly came from valid reasoning paths rather than lucky guesses. This suggests that pass@k at large values reliably indicates a model's true reasoning boundary.

These findings align with insights from reinforcing thinking through reasoning-enhanced reward models, which highlight the importance of understanding what RLVR is actually optimizing in LLMs.

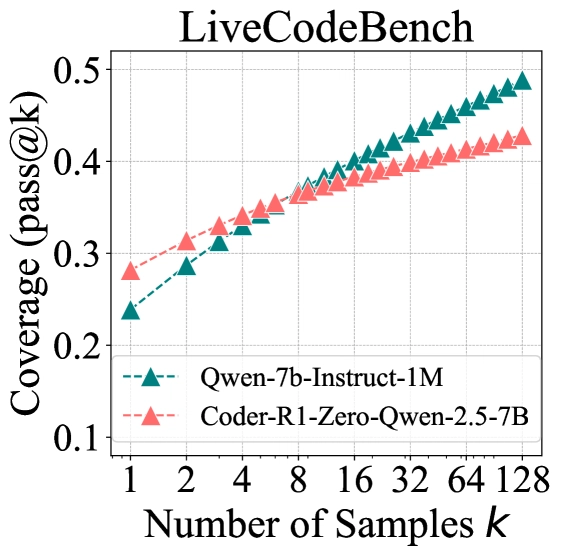
Code Generation: Confirming the Pattern

For code generation, the researchers evaluated Code-R1's RLVR-trained model (based on Qwen2.5-7B-Instruct) on LiveCodeBench v5, HumanEval+, and MBPP+.

Graph showing the performance pattern in code generation tasks comparing base and RLVR models.

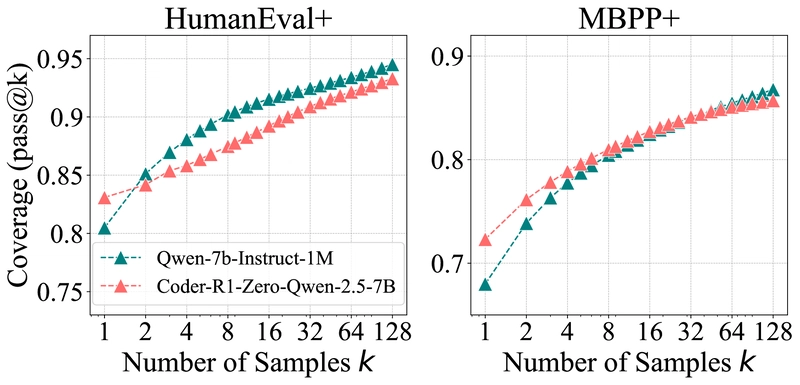
The results mirror the mathematical reasoning findings. On LiveCodeBench, the original model achieves a pass@1 score of 23.8%, while the RLVR-trained model reaches 28.1%. However, at k=128, approximately 50% of coding problems were solved by the original model compared to only 42.8% by the RLVR model.

Notably, the base model's curve continues to rise steeply at k=128, suggesting further improvement potential with more samples. In contrast, the RLVR model's curve flattens, indicating a narrower coverage boundary.

Graphs showing pass@k curves for both code generation and visual reasoning tasks, demonstrating the consistent pattern across domains.

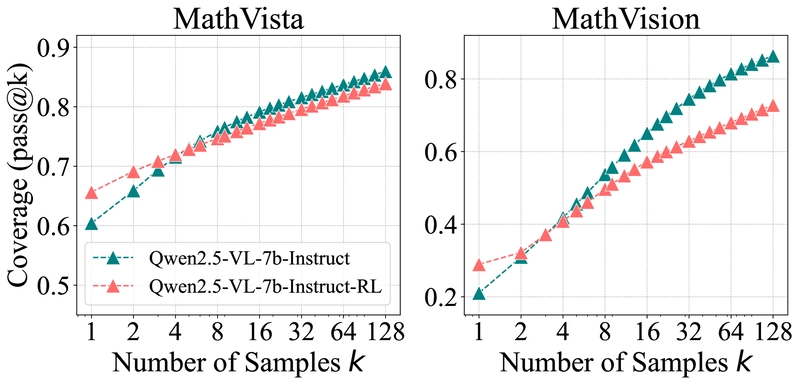
Visual Reasoning: The Pattern Persists in Multimodal Tasks

The visual reasoning experiments used the EasyR1 framework to train Qwen-2.5-VL-7B on Geometry3K, evaluating on filtered versions of MathVista-TestMini and MathVision-TestMini. Multiple-choice questions were removed to avoid simple guessing advantages.

The results confirm the same pattern observed in other domains: original models outperform RLVR models at large k values. Manual inspection of challenging problems verified that the performance increase was due to valid reasoning paths rather than lucky guesses.

This consistency across mathematical, code, and visual reasoning tasks provides strong evidence that reinforcement learning doesn't fundamentally enhance reasoning capacity beyond what already exists in base models.

Understanding Why RLVR Fails to Expand Reasoning Boundaries

Base Models Already Contain Advanced Reasoning Patterns

A deeper analysis reveals that problems solvable by RLVR models form an approximate subset of those solvable by base models. On AIME24, almost all problems solved by the RL-trained model could also be solved by the base model with sufficient sampling.

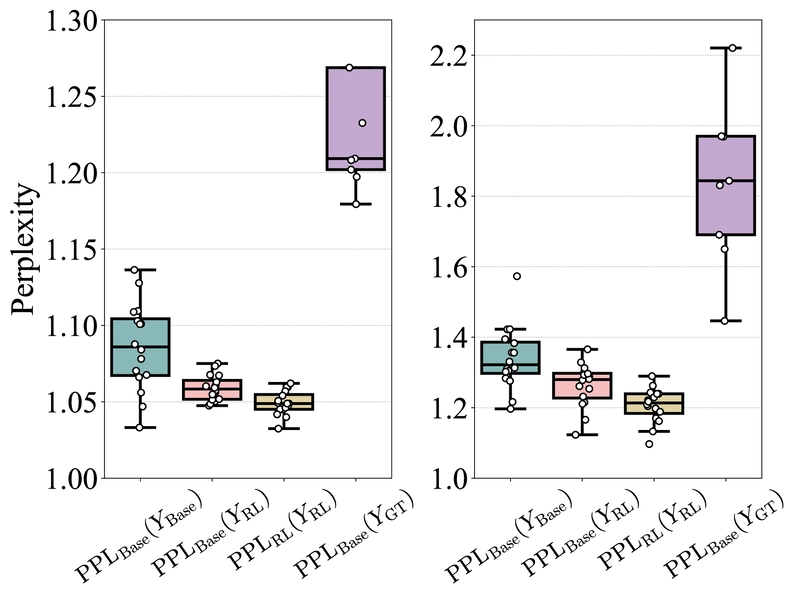
Left graph shows perplexity distribution of responses from different sources. Right graph compares coverage of base, instruct, RL, and distilled models.

The perplexity analysis reveals that responses from RL-trained models closely match the lower portion of the base model's distribution - corresponding to responses the base model would likely generate. This suggests that RLVR doesn't create new reasoning capabilities but rather biases the model toward paths it already encodes.

Three key conclusions emerge:

RLVR doesn't elicit novel reasoning: All reasoning paths used by RL models already exist within their base models, confirmed by pass@k at large values and perplexity distributions.
RLVR improves sampling efficiency: By biasing output distribution toward high-reward responses, RL increases the likelihood of sampling correct reasoning paths already encoded in the base model.
RLVR narrows the reasoning boundary: The efficiency gain comes at the expense of coverage, as RL training reduces output entropy and limits exploration.

These findings align with research on does reinforcement learning really incentivize reasoning capacity, which questions the conventional understanding of how RL training affects LLMs.

Distillation Expands the Reasoning Boundary

Unlike RLVR, distillation from powerful reasoning models can genuinely expand a model's reasoning capabilities. The researchers compared DeepSeek-R1-Distill-Qwen-7B (distilled from DeepSeek-R1 into Qwen-2.5-Math-7B) with the base model, its RL-trained counterpart, and an instruction-tuned version.

The distilled model consistently outperformed the base model across all k values, indicating that distillation introduces new reasoning patterns learned from the stronger teacher model. This fundamentally differentiates distillation from RLVR, which remains bounded by the base model's capabilities.

Comparing Different RL Algorithms: Similar Limitations

Graphs comparing different RL algorithms (top) and training steps (bottom), showing performance at different k values.

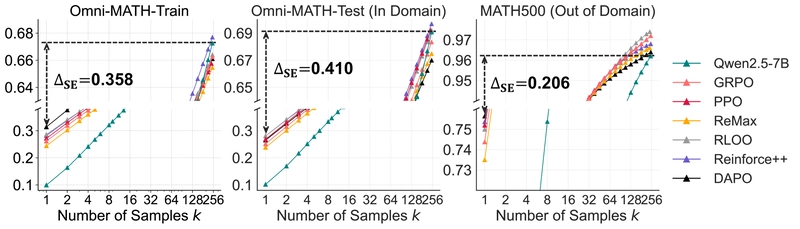
To quantify RLVR's effect on sampling efficiency, the researchers introduced the Sampling Efficiency Gap (ΔSE) - the difference between an RL model's pass@1 and its base model's pass@256. Lower ΔSE indicates better sampling efficiency.

Comparing popular RL algorithms (PPO, GRPO, Reinforce++, RLOO, ReMax, and DAPO) shows that while they exhibit slight variations, the differences aren't fundamental. ΔSE consistently remains above 40 points across algorithms, suggesting that current approaches are far from optimal and that novel methods may be needed to approach the theoretical upper bound.

Model	Omni-MATH-Train		Omni-MATH-Test		MATH500
	9.9	67.2	10.2	69.1	34.5	96.2
GRPO	26.1	66.3	25.1	68.3	74.4	97.2
PPO	27.2	65.8	26.8	69.2	75.2	97.2
ReMax	24.4	65.5	23.8	67.5	73.5	96.6
RLOO	28.6	66.4	28.1	69.2	75.0	97.4
Reinforce++	28.2	67.7	28.0	69.7	75.4	96.8
DAPO	31.4	66.1	26.5	67.0	75.6	96.4

Table 2: Detailed values for each point at pass@1 and pass@256 across different RL algorithms in Figure 7.

Notably, DAPO achieved slightly higher pass@1 scores but required 3-6 times more samples during training and showed significant performance drops at k=256. RLOO and Reinforce++ performed consistently well across all k values while maintaining efficient training costs. ReMax showed lower performance, likely due to its less stable advantage estimation in binary reward settings.

The Diminishing Returns of Extended RL Training

Model	Omni-MATH-Train		Omni-MATH-Test		MATH500
	9.9	67.2	10.2	69.1	34.5	96.2
GRPO-step150	26.1	66.3	25.1	68.3	74.4	97.2
GRPO-step300	33.6	65.3	27.1	66.6	75.4	96.0
GRPO-step450	42.5	64.3	28.3	63.9	76.3	95.4

Table 3: Detailed values at pass@1 and pass@256 across different RL training steps in Figure 7.

As RL training progresses, pass@1 on the training set consistently improves (from 26.1 to 42.5), but several concerning trends emerge:

Improvement on test sets (both in-domain and out-of-domain) slows dramatically after 150 steps, suggesting potential overfitting to the training data.
Pass@256 decreases across all datasets as training steps increase, indicating a shrinking reasoning boundary.

This suggests that longer training reduces the model's output entropy and exploration ability, further constraining its reasoning capacity.

Why RLVR Cannot Break Base Model Boundaries

Two key differences distinguish RLVR for LLMs from traditional reinforcement learning applications like AlphaGo Zero:

Vast Action Space: The language model action space is exponentially larger than in games like Go or Atari. RL algorithms weren't originally designed for such enormous spaces, making effective exploration nearly impossible from scratch.
Pretrained Priors: Unlike traditional RL that starts from scratch, RLVR begins with a pretrained model containing useful priors. This guides the model toward reasonable responses, enabling positive reward feedback.

These priors function as a double-edged sword. While they facilitate initial learning, they also constrain exploration. In such a complex space, most responses generated during training follow the base model's prior. Deviations are likely to produce invalid outputs with negative rewards.

Policy gradient algorithms maximize the likelihood of rewarded responses within the prior while minimizing the likelihood of unrewarded responses outside it. Consequently, the trained policy produces responses already present in the prior, constraining reasoning within the base model's boundaries.

This insight suggests that emerging medical reasoning from RLVR and other specialized applications may be limited by the boundaries of their base models, regardless of how extensive the RLVR training is.

Future approaches may need to explore beyond the confines of the prior or develop alternative paradigms beyond pure RLVR to truly enhance reasoning capabilities.

Situating This Work in the Broader Research Landscape

The post-training phase has proven crucial for enhancing LLM problem-solving abilities. Traditional approaches include supervised fine-tuning using human-curated data, self-improvement iteration, and reinforcement learning.

RLVR has gained significant traction for improving reasoning in mathematics and programming domains. OpenAI's o1 model pioneered large-scale RL for reasoning, followed by Deepseek-R1, which introduced the "zero" setting - applying reinforcement learning directly to base LLMs without intermediate supervised tuning.

This sparked numerous open-source efforts to replicate or extend R1's methodology and improve RL algorithms. In parallel, reinforcement learning has gained attention in multimodal reasoning.

Despite these advances, deep understanding of RLVR's effects on LLM reasoning and its limitations has been lacking. Previous research has noted that reflective behaviors in RLVR models emerge from base models rather than from RL training, but this study goes further - systematically demonstrating that all reasoning paths are already embedded in base models and that RLVR doesn't elicit fundamentally new reasoning capabilities.

Reimagining the Future of LLM Reasoning Enhancement

RLVR has been widely regarded as a promising approach for enabling LLMs to continuously self-improve and acquire novel reasoning abilities. However, this research conclusively demonstrates that RLVR doesn't elicit fundamentally new reasoning patterns.

Models	Problem Indices
Qwen-7B-Base	0,1,4,6,7,8,9,11,12,14,15,16,17,18,19,22,23,24,25,26,27,28,29
SimpleRL-Qwen-7B	0,1,6,7,8,9,12,14,15,16,18,22,23,24,25,26,27,28,29

Table 4: Indices of solvable problems in AIME24 (starting from 0). An approximate subset relationship can be observed: most problems solved by the RL model are also solvable by the base model.

Instead, RL primarily enhances sampling efficiency - making models more likely to generate correct reasoning paths that are already encoded in base models. This efficiency gain comes at the cost of coverage, as the reasoning boundary remains limited by base model capabilities.

Current RL algorithms remain far from achieving optimal sampling efficiency, defined by the reasoning boundary of base models. In contrast, distillation plays a significant role in introducing genuinely new reasoning patterns and expanding reasoning boundaries.

These findings highlight a critical limitation in current approaches to advancing LLM reasoning and suggest that new paradigms may be necessary to truly surpass base model capabilities. For researchers and practitioners exploring the frontiers of AI reasoning, this work provides crucial insights into the fundamental mechanisms and limitations of reinforcement learning in language models.

Graph showing pass@k performance on the filtered AIME24 dataset, reinforcing the main findings.

Click here to read the full summary of this paper