Qiskit Aer vs MQT DDSIM

Introduction Hi there, this article is about qiskit_aer and mqt.ddsim, both Python libraries for quantum computing to simulate quantum circuits on one's laptop. qiskit_aer is known as high-performance quantum computing simulators with realistic noise models [Qiskit Aer documentation]. Meanwhile, mqt.ddsim is a graph-based simulator, which reported that its efficiency had outperformed some of the existing simulators in a proposal paper, Advanced Simulation of Quantum Computations (the preprint is also available). By the way, as you already know or will find easily enough, both simulators have several modes. In this article, I only focus on their Quantum Assembly Language (QASM) simulators. I was wondering which one was faster. Thus, I performed a quick experiment and noted down the result here. Some of these parts are still a little ambitious for me. Please feel free to comment if you find any mistakes or places for suggested improvements. Experimental Result This section is for the people who would like to know the result first. Life is busy and the less time it takes to do things, the more time we have for more things to do, especially for things like this kind of random article. In my limited experimental settings, mqt.ddsim significantly outperformed qiskit_aer. The following graphs show you how much faster mqt.ddsim was. (Left) The figure of the average success probabilities. Qiskit Aer does not work with 31 qubits on my laptop whose specs will be noted later. (Right) The figure of the average execution times when the number of qubits is increased. From 25 qubits, the execution times by Qiskit Aer significantly increase. (Left) The figure of the average success probabilities. (Right) The figure of the average execution times when the number of adders is increased. The times by Qiskit Aer linearly grow up. The specs of my laptop are as follows. OS: MacBook Air Chip: M1 Memory: 16 GB I conducted the first experiment, which shows the time vs the number of qubits, with a quantum circuit having only one adder based on quantum Fourier transformation. For the second experiment, which shows the time vs the number of adders, I fixed the number of qubits as 21 since 21 is the largest number of qubits with which qiskit_aer works relatively fast. Also, I employed an adder for this experiment because adder is one of the fundamental blocks for quantum arithmetics. One can construct other arithmetics such as multiplication and exponentiation (e.g., [Circuit for Shor's algorithm using 2n+3 qubits (the preprint)]). It is worth noting that mqt.ddsim is known for taking significant time if the circuit is the absolute worst case as reported in the original paper. Quantum Computing Hereafter, I’ll write some introductions to quantum computing and show the result again with a little bit more of an in-depth explanation. First, we need to know what quantum computing is and the answer is computing with a quantum computer. That’s pretty easy, isn’t it? Then, one probably wonders what a quantum computer is. It is a computer based on quantum mechanics. The difference between classical and quantum computers is what they are based on. Whilst quantum computers work in a quantum manner, classical computers, which are computers we use every day, work based on classical physics. Unfortunately, my knowledge is limited here, so I cannot precisely explain the difference between them, but the important thing is that quantum mechanics have strange yet powerful phenomena to promise that quantum computing is faster than classical computing for certain fields and problems. One should be aware of this. Not everything works better with quantum computers, but some things work better with quantum computers and one finds significant improvements in them. However, our actual quantum computers are extremely limited compared to the theoretical results. Our current classical computers have a large number of bits, which are the fundamental units to store every data, and the error correction ability. That’s why we comfortably use our laptops for everyday use. The current quantum computers have a small number of qubits, which are the quantum version of bit, and small, or as far as I know, no error correction. That’s why it is quite difficult to conduct physical experiments involving a large number of qubits at this era called Noisy Intermediate-Scale Quantum (NISQ). We all are waiting for the era of Fault-Tolerant Quantum Computing (FTQC), which allows us to use more qubits with error correction techniques. Although we are in the era of NISQ, there are some things we can do with our laptops. One of these is simulation. Simulating quantum computers, more precisely quantum circuits, is one of the ways to see how proposed quantum algorithms work. But, as you might expect, simulating is not efficient at all. As one qubit is represented by a two-dimensional vector, to take $n$ qubits into account, we

Apr 8, 2025 - 03:37

Introduction

Hi there, this article is about qiskit_aer and mqt.ddsim, both Python libraries for quantum computing to simulate quantum circuits on one's laptop. qiskit_aer is known as high-performance quantum computing simulators with realistic noise models [Qiskit Aer documentation]. Meanwhile, mqt.ddsim is a graph-based simulator, which reported that its efficiency had outperformed some of the existing simulators in a proposal paper, Advanced Simulation of Quantum Computations (the preprint is also available).

By the way, as you already know or will find easily enough, both simulators have several modes. In this article, I only focus on their Quantum Assembly Language (QASM) simulators.

I was wondering which one was faster. Thus, I performed a quick experiment and noted down the result here.

Some of these parts are still a little ambitious for me. Please feel free to comment if you find any mistakes or places for suggested improvements.

Experimental Result

This section is for the people who would like to know the result first. Life is busy and the less time it takes to do things, the more time we have for more things to do, especially for things like this kind of random article.

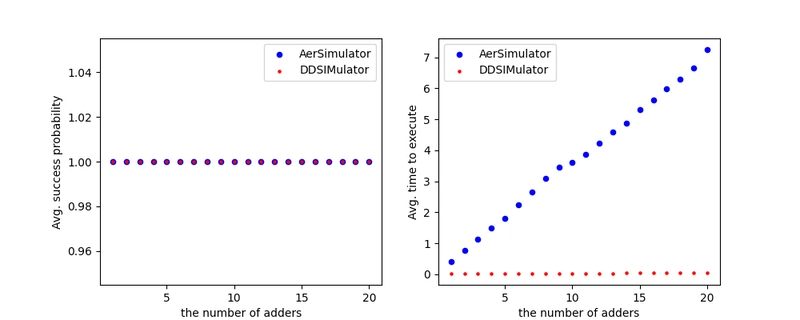
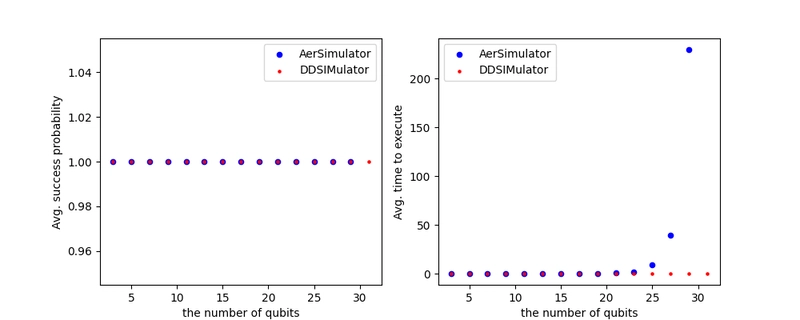
In my limited experimental settings, mqt.ddsim significantly outperformed qiskit_aer. The following graphs show you how much faster mqt.ddsim was.

(Left) The figure of the average success probabilities. Qiskit Aer does not work with 31 qubits on my laptop whose specs will be noted later. (Right) The figure of the average execution times when the number of qubits is increased. From 25 qubits, the execution times by Qiskit Aer significantly increase.

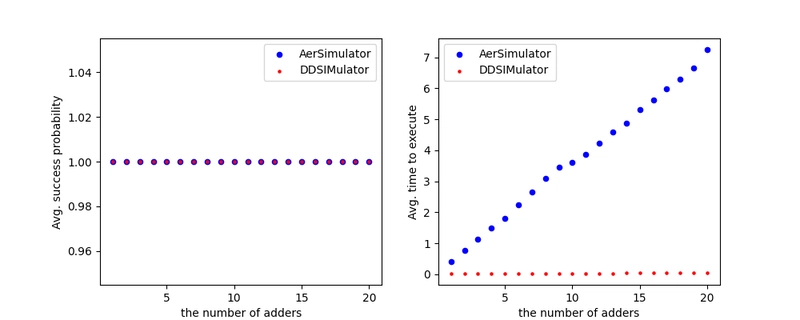
(Left) The figure of the average success probabilities. (Right) The figure of the average execution times when the number of adders is increased. The times by Qiskit Aer linearly grow up.

The specs of my laptop are as follows.

OS: MacBook Air
Chip: M1
Memory: 16 GB

I conducted the first experiment, which shows the time vs the number of qubits, with a quantum circuit having only one adder based on quantum Fourier transformation. For the second experiment, which shows the time vs the number of adders, I fixed the number of qubits as 21 since 21 is the largest number of qubits with which qiskit_aer works relatively fast.

Also, I employed an adder for this experiment because adder is one of the fundamental blocks for quantum arithmetics. One can construct other arithmetics such as multiplication and exponentiation (e.g., [Circuit for Shor's algorithm using 2n+3 qubits (the preprint)]).

It is worth noting that mqt.ddsim is known for taking significant time if the circuit is the absolute worst case as reported in the original paper.

Quantum Computing

Hereafter, I’ll write some introductions to quantum computing and show the result again with a little bit more of an in-depth explanation.

First, we need to know what quantum computing is and the answer is computing with a quantum computer. That’s pretty easy, isn’t it? Then, one probably wonders what a quantum computer is. It is a computer based on quantum mechanics. The difference between classical and quantum computers is what they are based on. Whilst quantum computers work in a quantum manner, classical computers, which are computers we use every day, work based on classical physics. Unfortunately, my knowledge is limited here, so I cannot precisely explain the difference between them, but the important thing is that quantum mechanics have strange yet powerful phenomena to promise that quantum computing is faster than classical computing for certain fields and problems. One should be aware of this. Not everything works better with quantum computers, but some things work better with quantum computers and one finds significant improvements in them.

However, our actual quantum computers are extremely limited compared to the theoretical results. Our current classical computers have a large number of bits, which are the fundamental units to store every data, and the error correction ability. That’s why we comfortably use our laptops for everyday use. The current quantum computers have a small number of qubits, which are the quantum version of bit, and small, or as far as I know, no error correction. That’s why it is quite difficult to conduct physical experiments involving a large number of qubits at this era called Noisy Intermediate-Scale Quantum (NISQ). We all are waiting for the era of Fault-Tolerant Quantum Computing (FTQC), which allows us to use more qubits with error correction techniques.

Although we are in the era of NISQ, there are some things we can do with our laptops. One of these is simulation. Simulating quantum computers, more precisely quantum circuits, is one of the ways to see how proposed quantum algorithms work. But, as you might expect, simulating is not efficient at all. As one qubit is represented by a two-dimensional vector, to take $n$ qubits into account, we need a $2^n$-dimensional vector, which goes up really easily. To make it more efficient to simulate it, several types of simulators have been proposed.

Qiskit

We saw what quantum computing is and why simulators are needed in the previous section. In this section, we’ll see then how we can actually write a program for working with quantum computers.

There are several ways to get on quantum computers. One of them is Qiskit. It is an open-source SDK for working with quantum computers. This is a Python library to write the programs. As we are in the NISQ era, it allows us to simulate the program on our laptops and also to work with IBM’s actual quantum computers. The latter one is super cool. However, actual quantum computers are not the main topic here. There are several ways to simulate the programs on your laptop. Qiskit itself has some of them. Also, there is Qiskit Aer, which is still in the Qiskit project but is separately installed from Qiskit itself now. Qiskit Aer is provided as high-performance quantum computing simulators with realistic noise models. As another option, I just found MQT DDSIM. MQT DDSIM is known as a graph-based simulator and it has experimentally shown that it outperformed other existing simulators in the original paper. It is noteworthy that their theoretical worst case is significantly worse than some of the other existing methods, which are called array-based. But, anyway, they showed that within their experiments, their proposal was the best.

So, I am wondering which one is better, Qiskit Aer or MQT DDSIM. I have got to admit that I could not find what the Qiskit Aer is based on. So, technically, it could be one of the methods that the DDSIM’s authors had compared with their method. But, well, it has also been a while since the paper came out and Qiskit Aer is constantly maintained. So, I believe it was worth it to conduct some experiments.

Results

I conducted the following experiments with my laptop whose specs are

OS: MacBook Air
Chip: M1
Memory: 16 GB

As I mentioned in one of the previous sections, there are several types of simulators in qiskit_aer and mqt.ddsim. However, I compared only qiskit_aer.AerSimulator and ddsim.qasmsimulator.QasmSimulatorBackend.

Execution time vs the number of qubits

In this experiment, I investigated the relation between the execution time and the number of qubits. For that, I employed qiskit.circuit.library.DraperQFTAdder. Quantum adders are one of the fundamental blocks for other arithmetic circuits and arithmetics are one of the fundamental sub-routines of some quantum algorithms. Thus, I believe that it is not the worst choice. qiskit.circuit.library.DraperQFTAdder takes the number of state qubits, which is the number of bits in each input register, as an argument. We observe the execution time whilst varying the number of state qubits. Also, I set “half” in kind argument. This setting adds another qubit to the circuit to prevent it from overflowing. Hence the number of qubits included in the circuit is $2n+1$, where $n$ is the number of state qubits. The experiments for each number of qubits were performed 10 times and are represented by the average in the graphs below.

The result of this experiment is as follows.

The left graph shows that both AerSimulator and QasmSimulatorBackend correctly added numbers in every number of qubits I attempted. However, because of the limited memory of my laptop, AerSimulator wasn’t able to simulate the circuit whilst QasmSimulatorBackend was. The right graph shows that the QasmSimulatorBackend constantly simulated the adder very fast whilst the execution times of AerSimulator shot up. As AerSimulator didn’t work with 31 qubits, the last blue point represents the execution time, around 250 secs, with $29 (= 2 * 14 + 1)$.

The only adder is not much in terms of how many gates are used in one circuit, yet AerSimulator didn’t manage to handle this.

Execution time vs the number of adders

In this experiment, I investigated the relation between the execution time and the number of adders with a fixed number of qubits, which is 21. I employed 21 from the previous result; it is relatively large yet the execution times of them are still quite close at least on the graph. As an adder, qiskit.circuit.library.DraperQFTAdder is again employed. This time, I applied this adder multiple times and saw how much time the two simulators took. The experiments for each number of qubits were performed 10 times and are represented by the average in the graphs below.

The result is as follows.

Again, even if multiple adders were applied, the left graph shows that they both correctly simulated. The right graph shows that AerSimulator took linear time to execute the circuit when the number of adders was increased. Meanwhile, QasmSimulatorBackend took (at least from the graph) almost constant time.

Additional experiments on DDSIM

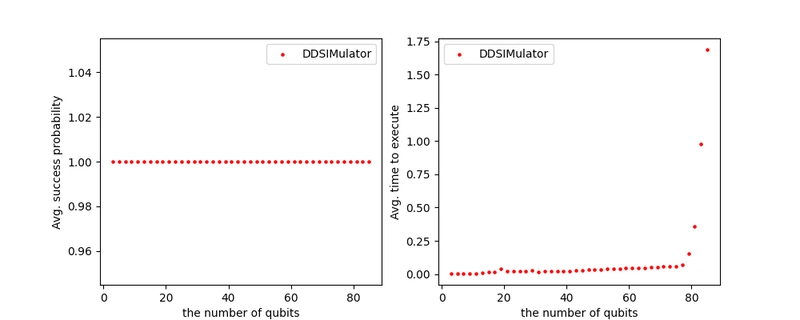
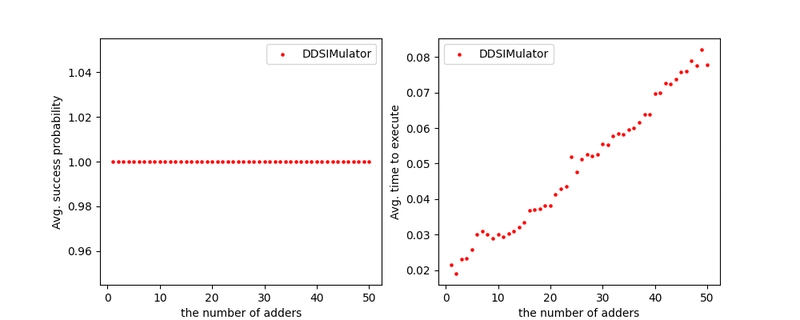
The graphs above show that QasmSimulatorBackend works in almost constant time. I wondered if the experimental settings allow the simulator to work in exactly constant time in theory. Thus, I conducted additional two experiments for both settings. I performed the same experiments on QasmSimulatorBackend but with additional cases.

As the graphs show, both settings can be difficult to run on a personal laptop. Specifically, it took more than a day to finish to perform the experiment with 101 qubits settings so I had to cancel the experiment and be compromised with 85 qubits.

Conclusion and a little bit more

I conducted easy experiments with adders suggested by Draper on my personal Mac M1 laptop with 16GB memory to see the speed difference between QASM simulators of qiskit_aer and mqt.ddsim. As a result, mqt.ddsim simulated the circuits much faster than qiskit_aer. Moreover, I performed an additional experiment with only mqt.ddsim. The additional experiment is to

Verify the settings are not too good for mqt.ddsim since the previous experiments looked like mqt.ddsim simulated every circuit in the settings in almost constant time and I suspected that the settings might allow it to work in constant time.
See the limitation if the settings do not allow it to work in constant time.

As I wrote this several times, all the experiments are quite limited in terms of the circuits that I employed. Hence, one cannot determine that mqt.ddsim is absolutely better than qiskit_aer from the experiment. However, the result gives us an idea that at least there are cases where mqt.ddsim is significantly faster.

For future investigation, it'd be nice to perform experiments with richer circuits, for instance, more complex arithmetics as well as multiple rotation gates. Rotation gates are often used in the field of quantum machine learning, especially in Variational Quantum Classifiers (VQCs). Most of those models were invented to work with the NISQ era. Thus, it is relatively easy to perform experiments, yet because of the number of data, it's not the easiest to access actual quantum computers. Therefore, simulating those quantum machine learning algorithms is still one of the main ways to measure performance.

All the experiments and everything has be done with jupyter notebook and the notebook is in https://github.com/ksk0629/backend_comparison.

By the way, I met MQT DDSIM when I was reading Choco-Q: Commute Hamiltonian-based QAOA for Constrained Binary Optimization and checking their implementations. This is completely on a different topic here, yet the paper was really interesting.