GEN-AI 5 : WGAN and WGAN-GP

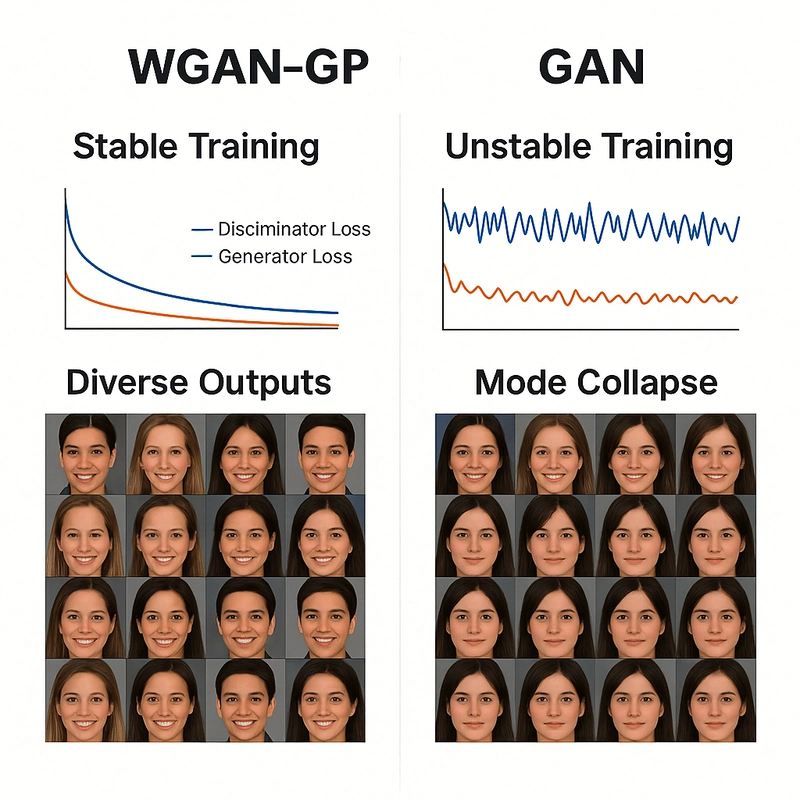
Why ❌ GAN In the ever-evolving landscape of generative models, GANs have taken center stage with their remarkable ability to generate data that mimics real-world distributions. But as with all great things, classic GANs came with caveats—training instability, vanishing gradients, and mode collapse, to name a few. Let’s dive deeper into these powerful models: WGAN and its enhanced cousin WGAN-GP, two sophisticated upgrades that fix many of GANs' shortcomings. What is Wasserstein distance Wasserstein Distance, also known as the Earth Mover's Distance (EMD), is a mathematical measure of the distance between two probability distributions. Imagine you have two piles of sand—one symbolizing real data and the other representing data generated by a model. The goal is to reshape one pile into the other by moving portions of sand. The effort required depends not only on how much sand you move but also on how far you move it. This effort is what the Wasserstein Distance measures—a cost-efficient way to transform one distribution into another. What makes this distance especially powerful is its ability to compare distributions even when they don't overlap at all—a situation where traditional measures like JS divergence fail. It offers a continuous and interpretable signal for how "far off" the generated data is from the real data, making it incredibly useful for training generative models like WGANs. Traditional GANs use Jensen-Shannon (JS) divergence to measure similarity between distributions. BUT : JS divergence becomes undefined or uninformative when distributions don't overlap. This leads to vanishing gradients—a huge problem for training By contrast, Wasserstein Distance: Remains well-defined and continuous even when distributions are far apart. Provides meaningful gradients, allowing the generator to learn effectively from the start. Improvement in WGAN wrt GAN WGAN is a variant of GAN that uses the Wasserstein Distance as its loss function instead of JS divergence. Key differences from traditional GAN: The discriminator is now called a critic. It doesn't classify data as real/fake, but scores it to reflect how “real” it looks. The loss function is based on the difference in critic scores for real vs. fake data. In simple terms: Real Data → High Critic Score Fake Data → Low Critic Score The generator improves by producing data that the critic scores higher. Working Just like in standard GANs, WGAN consists of two neural networks: A Generator (G) that tries to generate realistic data from random noise. A Critic (C) (not called a discriminator here) that scores the realness of data, assigning higher values to real data and lower values to fake ones. Unlike GANs, which use a sigmoid function to classify samples as real or fake, WGAN's critic outputs real-valued scores—this small shift changes everything. The Loss Function The heart of WGAN lies in replacing Jensen-Shannon divergence with the Wasserstein distance (also called Earth Mover’s Distance)—a metric that measures how much "effort" it takes to morph the generated distribution into the real one. This results in the following loss functions: Critic's Loss:

Apr 20, 2025 - 02:45

Why ❌ GAN

In the ever-evolving landscape of generative models, GANs have taken center stage with their remarkable ability to generate data that mimics real-world distributions. But as with all great things, classic GANs came with caveats—training instability, vanishing gradients, and mode collapse, to name a few.

Let’s dive deeper into these powerful models: WGAN and its enhanced cousin WGAN-GP, two sophisticated upgrades that fix many of GANs' shortcomings.

What is Wasserstein distance

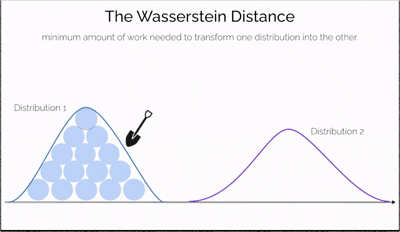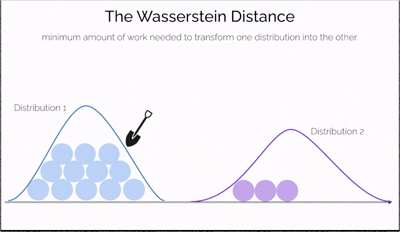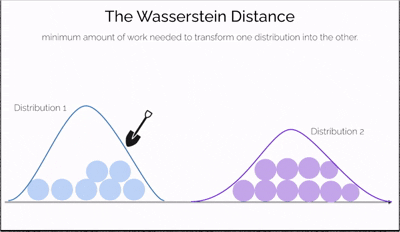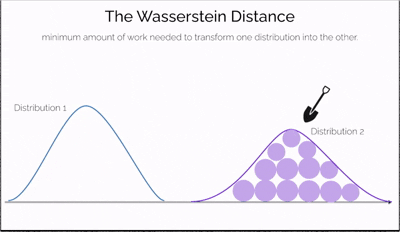
Wasserstein Distance, also known as the Earth Mover's Distance (EMD), is a mathematical measure of the distance between two probability distributions.

Imagine you have two piles of sand—one symbolizing real data and the other representing data generated by a model. The goal is to reshape one pile into the other by moving portions of sand. The effort required depends not only on how much sand you move but also on how far you move it. This effort is what the Wasserstein Distance measures—a cost-efficient way to transform one distribution into another.

What makes this distance especially powerful is its ability to compare distributions even when they don't overlap at all—a situation where traditional measures like JS divergence fail. It offers a continuous and interpretable signal for how "far off" the generated data is from the real data, making it incredibly useful for training generative models like WGANs.

Traditional GANs use Jensen-Shannon (JS) divergence to measure similarity between distributions.
BUT :

JS divergence becomes undefined or uninformative when distributions don't overlap.
This leads to vanishing gradients—a huge problem for training

By contrast, Wasserstein Distance:

Remains well-defined and continuous even when distributions are far apart.
Provides meaningful gradients, allowing the generator to learn effectively from the start.

Improvement in WGAN wrt GAN

WGAN is a variant of GAN that uses the Wasserstein Distance as its loss function instead of JS divergence.

Key differences from traditional GAN:
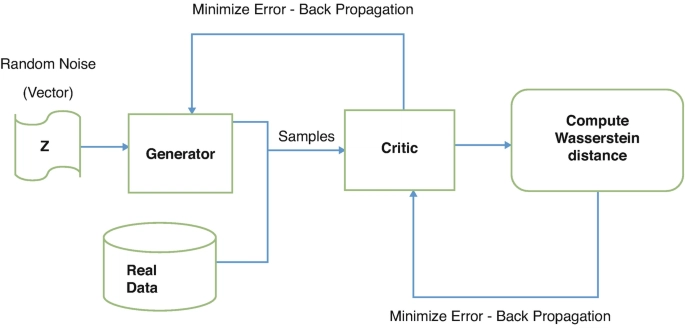
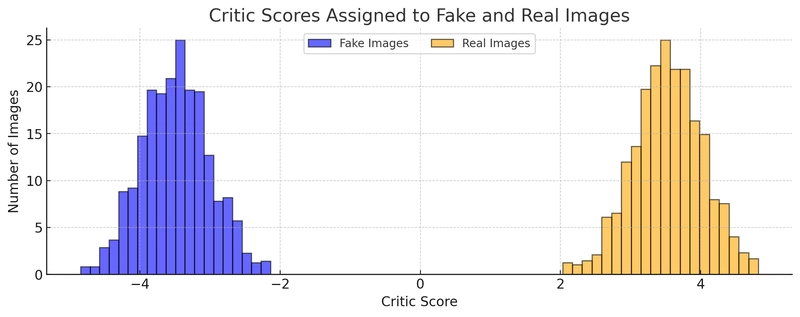
The discriminator is now called a critic. It doesn't classify data as real/fake, but scores it to reflect how “real” it looks.

The loss function is based on the difference in critic scores for real vs. fake data.

In simple terms:
Real Data → High Critic Score
Fake Data → Low Critic Score
The generator improves by producing data that the critic scores higher.

Working

Just like in standard GANs, WGAN consists of two neural networks:

A Generator (G) that tries to generate realistic data from random noise.
A Critic (C) (not called a discriminator here) that scores the realness of data, assigning higher values to real data and lower values to fake ones.

Unlike GANs, which use a sigmoid function to classify samples as real or fake, WGAN's critic outputs real-valued scores—this small shift changes everything.

The Loss Function

The heart of WGAN lies in replacing Jensen-Shannon divergence with the Wasserstein distance (also called Earth Mover’s Distance)—a metric that measures how much "effort" it takes to morph the generated distribution into the real one.

This results in the following loss functions:

Critic's Loss: