From Fingers to Networks: Introduction to Binary and Hexadecimal
Preamble: This space will be utilized to synthesize my notes and help improve my learning process while I study for the CompTIA Network+ N10-009 certification exam. Please follow along for more Network+ notes and feel free to ask any questions or, if I get something wrong, offer suggestions to correct any mistakes. Understanding Number Systems in Networking: Decimal, Binary, and Hexadecimal In the world of computer networking, understanding different ways of counting is essential. We'll explore decimal, the system we use every day, and then dive into binary and hexadecimal, which are the languages of computers. These skills are fundamental to grasping concepts like IP addressing and subnetting, which you'll encounter throughout your networking journey for the CompTIA Network+ exam. Decimal Counting (Base 10) Decimal counting is what humans are most familiar with because we have a total of 10 fingers on our two hands. This system, also known as Base 10, uses ten unique digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Once we reach 9, we add another digit to the left to represent ten (10). In decimal, each digit's position has a value that is a power of 10. A digit positioned to the left of another has 10 times the value of the digit to its right. For example, the number 255 can be broken down as follows: (2×10^2)+(5×10^1)+(5×10^0)=(2×100)+(5×10)+(5×1)=200+50+5=255 Binary Counting (Base 2) Binary is the fundamental language of computers. It is a Base 2 system, meaning it only uses two digits: 0 and 1. Each position in a binary number represents a power of 2. Consider the binary value 11111111. To convert this to decimal, we calculate the sum of each digit multiplied by its corresponding power of 2, starting from the rightmost digit as 20: (1×2^7)+(1×2^6)+(1×2^5)+(1×2^4)+(1×2^3)+(1×2^2)+(1×2^1)+(1×20)= (1×128)+(1×64)+(1×32)+(1×16)+(1×8)+(1×4)+(1×2)+(1×1)=128+64+32+16+8+4+2+1=255 As you can see, it takes eight binary digits to represent a decimal value up to 255. An 8-bit value is called a byte or an octet. These groupings are important in computer memory and addressing. For example, an IPv4 address is often expressed as four decimal octets, where each octet represents 8 bits of binary information. The four decimal numbers in the SOHO router's WAN IP address 203.0.113.1 are examples of these octets. Ultimately, computers process these decimal numbers in their binary form. Let's take a small binary number, 101, as another example. To convert it to decimal: (1×2^2)+(0×2^1)+(1×2^0)=(1×4)+(0×2)+(1×1)=4+0+1=5 Hexadecimal Counting (Base 16) Hexadecimal, often shortened to "hex," is Base 16. It provides a more convenient way of representing long sequences of bytes used in various networking contexts, such as hardware MAC addresses. Hexadecimal uses 16 possible values for each digit, represented by the numerals 0 through 9 and the characters A, B, C, D, E, and F, where A represents 10, B represents 11, C represents 12, D represents 13, E represents 14, and F represents 15. You can see a useful conversion chart for decimal, hexadecimal, and binary below: As you can see, each hexadecimal digit easily corresponds to a 4-digit binary number called a nibble (although this term is not used as often anymore, it represents 4 bits). This direct relationship makes it simple to convert between hexadecimal and binary. This is the basics for understanding binary and hexadecimal. Keep this knowledge handy when we dive deeper into subnetting later on in these notes. If you are keen to further understand how to convert between decimal, binary, and hexadecimal, I highly recommend going through the following video from Paul Browning and getting a copy of his book “IP Subnetting: From Zero to Hero”: Paul Browning: Subnetting Zero to Hero Youtube Thanks for reading today’s notes about binary, decimal, and hexadecimal counting. Next time, we'll talk about the troubleshooting methodology that CompTIA (and the IT world at large) uses for solving issues related to computing. These skills are also highly transferable to any other type of troubleshooting in your life. See you then!
Preamble:
This space will be utilized to synthesize my notes and help improve my learning process while I study for the CompTIA Network+ N10-009 certification exam. Please follow along for more Network+ notes and feel free to ask any questions or, if I get something wrong, offer suggestions to correct any mistakes.
Understanding Number Systems in Networking: Decimal, Binary, and Hexadecimal
In the world of computer networking, understanding different ways of counting is essential. We'll explore decimal, the system we use every day, and then dive into binary and hexadecimal, which are the languages of computers. These skills are fundamental to grasping concepts like IP addressing and subnetting, which you'll encounter throughout your networking journey for the CompTIA Network+ exam.
Decimal Counting (Base 10)
Decimal counting is what humans are most familiar with because we have a total of 10 fingers on our two hands. This system, also known as Base 10, uses ten unique digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Once we reach 9, we add another digit to the left to represent ten (10).
In decimal, each digit's position has a value that is a power of 10. A digit positioned to the left of another has 10 times the value of the digit to its right. For example, the number 255 can be broken down as follows:
(2×10^2)+(5×10^1)+(5×10^0)=(2×100)+(5×10)+(5×1)=200+50+5=255
Binary Counting (Base 2)
Binary is the fundamental language of computers. It is a Base 2 system, meaning it only uses two digits: 0 and 1. Each position in a binary number represents a power of 2.
Consider the binary value 11111111. To convert this to decimal, we calculate the sum of each digit multiplied by its corresponding power of 2, starting from the rightmost digit as 20:
(1×2^7)+(1×2^6)+(1×2^5)+(1×2^4)+(1×2^3)+(1×2^2)+(1×2^1)+(1×20)=
(1×128)+(1×64)+(1×32)+(1×16)+(1×8)+(1×4)+(1×2)+(1×1)=128+64+32+16+8+4+2+1=255
As you can see, it takes eight binary digits to represent a decimal value up to 255. An 8-bit value is called a byte or an octet. These groupings are important in computer memory and addressing. For example, an IPv4 address is often expressed as four decimal octets, where each octet represents 8 bits of binary information. The four decimal numbers in the SOHO router's WAN IP address 203.0.113.1 are examples of these octets. Ultimately, computers process these decimal numbers in their binary form.
Let's take a small binary number, 101, as another example. To convert it to decimal:
(1×2^2)+(0×2^1)+(1×2^0)=(1×4)+(0×2)+(1×1)=4+0+1=5
Hexadecimal Counting (Base 16)
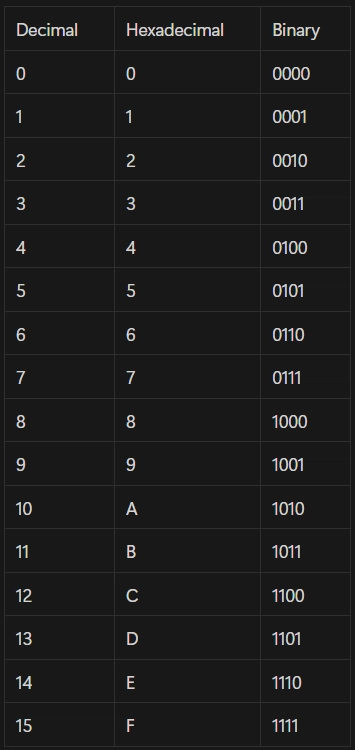
Hexadecimal, often shortened to "hex," is Base 16. It provides a more convenient way of representing long sequences of bytes used in various networking contexts, such as hardware MAC addresses. Hexadecimal uses 16 possible values for each digit, represented by the numerals 0 through 9 and the characters A, B, C, D, E, and F, where A represents 10, B represents 11, C represents 12, D represents 13, E represents 14, and F represents 15.
You can see a useful conversion chart for decimal, hexadecimal, and binary below:
As you can see, each hexadecimal digit easily corresponds to a 4-digit binary number called a nibble (although this term is not used as often anymore, it represents 4 bits). This direct relationship makes it simple to convert between hexadecimal and binary.
This is the basics for understanding binary and hexadecimal. Keep this knowledge handy when we dive deeper into subnetting later on in these notes. If you are keen to further understand how to convert between decimal, binary, and hexadecimal, I highly recommend going through the following video from Paul Browning and getting a copy of his book “IP Subnetting: From Zero to Hero”:
Paul Browning: Subnetting Zero to Hero Youtube
Thanks for reading today’s notes about binary, decimal, and hexadecimal counting. Next time, we'll talk about the troubleshooting methodology that CompTIA (and the IT world at large) uses for solving issues related to computing. These skills are also highly transferable to any other type of troubleshooting in your life. See you then!




























![[Webinar] AI Is Already Inside Your SaaS Stack — Learn How to Prevent the Next Silent Breach](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiOWn65wd33dg2uO99NrtKbpYLfcepwOLidQDMls0HXKlA91k6HURluRA4WXgJRAZldEe1VReMQZyyYt1PgnoAn5JPpILsWlXIzmrBSs_TBoyPwO7hZrWouBg2-O3mdeoeSGY-l9_bsZB7vbpKjTSvG93zNytjxgTaMPqo9iq9Z5pGa05CJOs9uXpwHFT4/s1600/ai-cyber.jpg?#)











































































































































![[The AI Show Episode 144]: ChatGPT’s New Memory, Shopify CEO’s Leaked “AI First” Memo, Google Cloud Next Releases, o3 and o4-mini Coming Soon & Llama 4’s Rocky Launch](https://www.marketingaiinstitute.com/hubfs/ep%20144%20cover.png)





























































































































![[FREE EBOOKS] Machine Learning Hero, AI-Assisted Programming for Web and Machine Learning & Four More Best Selling Titles](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)








































































![Rogue Company Elite tier list of best characters [April 2025]](https://media.pocketgamer.com/artwork/na-33136-1657102075/rogue-company-ios-android-tier-cover.jpg?#)







































































_Andreas_Prott_Alamy.jpg?width=1280&auto=webp&quality=80&disable=upscale#)






















































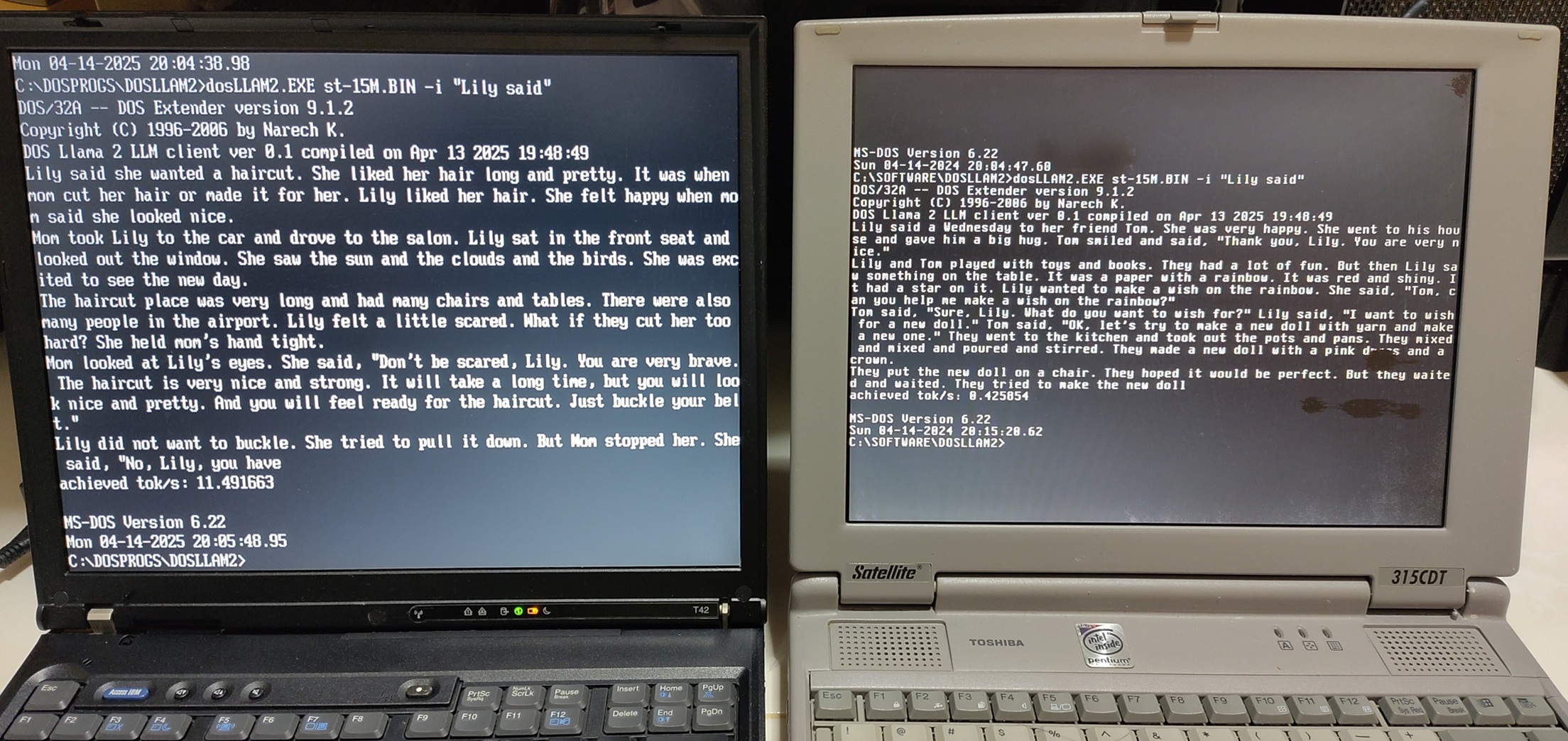



































![What’s new in Android’s April 2025 Google System Updates [U: 4/18]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2025/01/google-play-services-3.jpg?resize=1200%2C628&quality=82&strip=all&ssl=1)










![Apple Watch Series 10 Back On Sale for $299! [Lowest Price Ever]](https://www.iclarified.com/images/news/96657/96657/96657-640.jpg)
![EU Postpones Apple App Store Fines Amid Tariff Negotiations [Report]](https://www.iclarified.com/images/news/97068/97068/97068-640.jpg)
![Apple Slips to Fifth in China's Smartphone Market with 9% Decline [Report]](https://www.iclarified.com/images/news/97065/97065/97065-640.jpg)