Exploring elixir processes using merge sort

In this article, I use the word parallel and concurrent interchangeably. I need the readers to know that they are not the same. Parallel means solving smaller problems of the same chunk of work at the same time. Concurrent means solving multiple problems in what appears to be the same time. Sorting. A classic problem in computer science. We always need things in the right order for a variety of reasons. There are many sorting algorithms each with their merits and demerits and some made for the fun of it(I'm looking at you Bogosort). A popular algorithm is merge sort. This algorithm uses a divide and conquer approach, subdividing the list into individual elements and then merging those elements in the correct order. This is a great problem to teach yourself how to get around the recursive nature of functional languages like Elixir or Erlang. Elixir & its processes. Elixir runs on the Erlang VM, known for creating low latency, distributed, and fault-tolerant systems. Elixir Docs A cool thing that Elixir inherits from Erlang are its processes. All Elixir code runs inside processes that are isolated from each other, run concurrently and communicate via message passing. This allows Elixir developers to build distributed and fault tolerant processes. Of importance is the fact that Elixir processes are not Operating system processes. Instead, they are lightweight in terms of memory and CPU, which allows a programmer to run tens or even hundreds of thousands of processes running simultaneously.There is a limit to how many processes you can spawn though(definitely not foreshadowing) Light weight processes and merge sort Well, if we have the ability to spawn light weight processes, a functional language and a sorting algorithm which we may be able to parallelize, the obvious next step is to absolutely misuse all of these ingredients until we have a working algorithm, right? Let's cook Ok, if I recall from my multicore programming classes, the first thing you want to do when attempting to parallelize a problem that is sequential is to identify which parts of the algorithm can be done in parallel. So we look at the parts of merge sort Parts of the merge sort algorithm Find the mid-point of an array and divide the array into two halves, left and right Perform Mergesort on the left Perform Mergesort on the right Merge the two sorted halves(left and right) Implementation 1 What if in our first solution, every time we want to perform merge sort on a sub_array, we spawn a new process and let it handle that sorting for us? That sounds like a great idea. Let us do this: def psort([]), do: [] def psort([x]), do: [x] def psort(list) do {sub_arr1, sub_arr2} = Enum.split(list, floor(length(list) / 2)) parent = self() child1 = spawn(fn -> send(parent, {:sorted, self(), psort(sub_arr1)}) end) child2 = spawn(fn -> send(parent, {:sorted, self(), psort(sub_arr2)}) end) sorted_sub_arr1 = receive_sorted(child1) sorted_sub_arr2 = receive_sorted(child2) merge(sorted_sub_arr1, sorted_sub_arr2) end defp receive_sorted(child_pid) do receive do {:sorted, ^child_pid, sorted_list} -> sorted_list # {:die} -> # Process.exit(self(), :normal) end end def merge(l1, l2) do new_list = has_elements(l1, l2) new_list end def has_elements([], l2, c), do: Enum.reverse(c, l2) def has_elements(l1, [], c), do: Enum.reverse(c, l1) def has_elements([hd1 | r1], [hd2 | r2], c \\ []) do if hd1 > hd2 do has_elements([hd1 | r1], r2, [hd2 | c]) else has_elements(r1, [hd2 | r2], [hd1 | c]) end end Ok, that's a lot of code, but let us focus on this part: {sub_arr1, sub_arr2} = Enum.split(list, floor(length(list) / 2)) parent = self() child1 = spawn(fn -> send(parent, {:sorted, self(), psort(sub_arr1)}) end) child2 = spawn(fn -> send(parent, {:sorted, self(), psort(sub_arr2)}) end) We split the list into 2 sub_arrays and then spawn 2 processes to implement the merge_sort on those sub_arrays. `{:sorted, self(), psort(list)} is a message pattern that the parent process will expect to receive. You can read more about sending and receiving messages for processes in Elixir here Benchmarking implementation 1 vs a sequential sort algorithm. You only ever see the benefits of parallelization when you get some benchmarks and comparison. So let us compare our implementation with a sequential merge sort algorithm. In our benchmark, we do 40 runs of random lists with varying sizes for both the sequential and parallel implementations. Wait, that's not what we want. Our parallel execution is consistently slower, regardless of the number of elements. We wanted to see some form of efficiency. Why? Processes are not a free lunch Typically, parallelization will incur some overhead. Spawning process takes some time. Mess

Apr 15, 2025 - 00:25

Exploring elixir processes using merge sort

In this article, I use the word parallel and concurrent interchangeably. I need the readers to know that they are not the same. Parallel means solving smaller problems of the same chunk of work at the same time. Concurrent means solving multiple problems in what appears to be the same time.

Sorting.

A classic problem in computer science. We always need things in the right order for a variety of reasons. There are many sorting algorithms each with their merits and demerits and some made for the fun of it(I'm looking at you Bogosort). A popular algorithm is merge sort. This algorithm uses a divide and conquer approach, subdividing the list into individual elements and then merging those elements in the correct order. This is a great problem to teach yourself how to get around the recursive nature of functional languages like Elixir or Erlang.

Elixir & its processes.

Elixir runs on the Erlang VM, known for creating low latency, distributed, and fault-tolerant systems. Elixir Docs

A cool thing that Elixir inherits from Erlang are its processes. All Elixir code runs inside processes that are isolated from each other, run concurrently and communicate via message passing. This allows Elixir developers to build distributed and fault tolerant processes. Of importance is the fact that Elixir processes are not Operating system processes. Instead, they are lightweight in terms of memory and CPU, which allows a programmer to run tens or even hundreds of thousands of processes running simultaneously.There is a limit to how many processes you can spawn though(definitely not foreshadowing)

Light weight processes and merge sort

Well, if we have the ability to spawn light weight processes, a functional language and a sorting algorithm which we may be able to parallelize, the obvious next step is to absolutely misuse all of these ingredients until we have a working algorithm, right?

Let's cook

Ok, if I recall from my multicore programming classes, the first thing you want to do when attempting to parallelize a problem that is sequential is to identify which parts of the algorithm can be done in parallel. So we look at the parts of merge sort

Parts of the merge sort algorithm

Find the mid-point of an array and divide the array into two halves, left and right
Perform Mergesort on the left
Perform Mergesort on the right
Merge the two sorted halves(left and right)

Implementation 1

What if in our first solution, every time we want to perform merge sort on a sub_array, we spawn a new process and let it handle that sorting for us? That sounds like a great idea. Let us do this:

  def psort([]), do: []
  def psort([x]), do: [x]

  def psort(list) do
    {sub_arr1, sub_arr2} = Enum.split(list, floor(length(list) / 2))
    parent = self()

    child1 = spawn(fn -> send(parent, {:sorted, self(), psort(sub_arr1)}) end)
    child2 = spawn(fn -> send(parent, {:sorted, self(), psort(sub_arr2)}) end)

    sorted_sub_arr1 = receive_sorted(child1)
    sorted_sub_arr2 = receive_sorted(child2)

    merge(sorted_sub_arr1, sorted_sub_arr2)
  end

  defp receive_sorted(child_pid) do
    receive do
      {:sorted, ^child_pid, sorted_list} ->
        sorted_list

      # {:die} ->
      #   Process.exit(self(), :normal)
    end
  end

  def merge(l1, l2) do
    new_list = has_elements(l1, l2)
    new_list
  end

  def has_elements([], l2, c), do: Enum.reverse(c, l2)
  def has_elements(l1, [], c), do: Enum.reverse(c, l1)

  def has_elements([hd1 | r1], [hd2 | r2], c \\ []) do
    if hd1 > hd2 do
      has_elements([hd1 | r1], r2, [hd2 | c])
    else
      has_elements(r1, [hd2 | r2], [hd1 | c])
    end
  end

Ok, that's a lot of code, but let us focus on this part:

    {sub_arr1, sub_arr2} = Enum.split(list, floor(length(list) / 2))
    parent = self()

    child1 = spawn(fn -> send(parent, {:sorted, self(), psort(sub_arr1)}) end)
    child2 = spawn(fn -> send(parent, {:sorted, self(), psort(sub_arr2)}) end)

We split the list into 2 sub_arrays and then spawn 2 processes to implement the merge_sort on those sub_arrays. `{:sorted, self(), psort(list)} is a message pattern that the parent process will expect to receive. You can read more about sending and receiving messages for processes in Elixir here

Benchmarking implementation 1 vs a sequential sort algorithm.

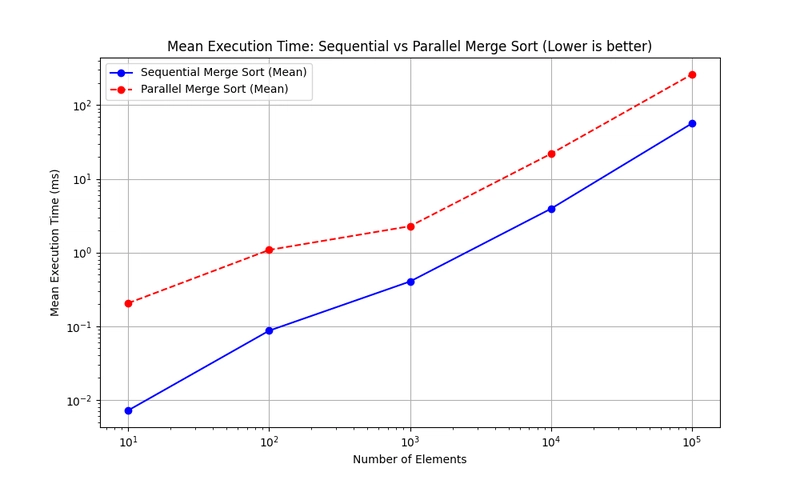
You only ever see the benefits of parallelization when you get some benchmarks and comparison. So let us compare our implementation with a sequential merge sort algorithm.

In our benchmark, we do 40 runs of random lists with varying sizes for both the sequential and parallel implementations.

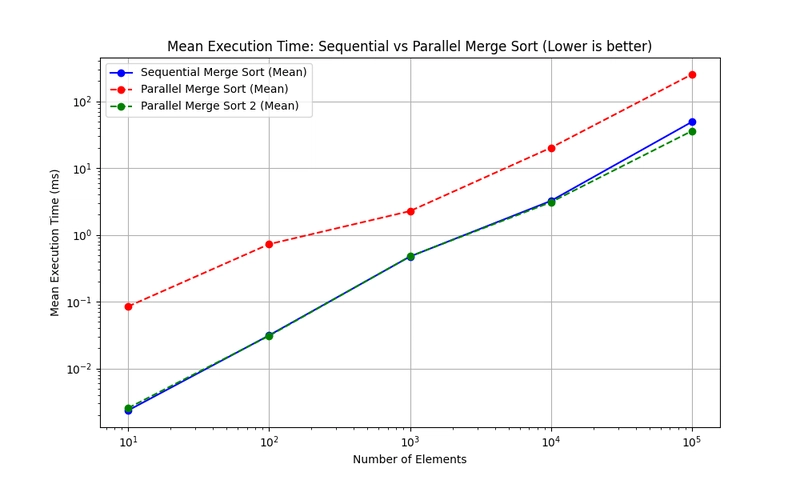
Wait, that's not what we want. Our parallel execution is consistently slower, regardless of the number of elements. We wanted to see some form of efficiency. Why?

Processes are not a free lunch

Typically, parallelization will incur some overhead. Spawning process takes some time. Message passing takes some more time. All the while the sequential algorithm just chugs along undisturbed(so to speak).

The way to use processes, it to use them when they would offer a clear benefit over a a sequential execution. So how do we do that?

Implementation 2

What if we kept the implementation 1 method, but only do it depending on the size of a list passed. This means that is we want to sort a list of 100 elements, we could do this sequentially, but if the list has 1_000_000 elements, perhaps we could split the load among multiple processes?

We add a simple check before splitting the array and instruct it to use our sequential merge sort implementation

if length(list) <= @list_threshold do SequentialMergeSort.seq_sort(list) else ... end
I set the threshold at 1000 elements in a list.

This gives us the following results.

What we notice is that all we end up with a similar trend to the sequential algorithm. Which means that we are not really getting any speed up. And if we are, it is practically negligible. Interestingly though, the initial parallel implementation fails when we get to 1 million elements in a list because we spawn too many processes. But the simple solution allows us to go up to a million with no ill effect. So there is some benefit, but there has to be a better improvement somewhere.

I will be working on this a bit more to find out more performance optimizations where I can find them. Feel free to checkout and contribute to the github repo.