Embeddings clustering with Agglomerative Hierarchical Clustering (messy-folder-reorganizer-ai)
Adding RAG and ML to Messy-Folder-Reorganizer-AI Why ML Methods for Clustering As we discovered in previous articles, all LLMs have context restrictions, so we cannot send hundreds of file names to an LLM and ask it to create folder names for all of them. On the other hand, sending a request for each file separately is not only inefficient and redundant—it also breaks the global context. For example, if you have files like bill_for_electricity.pdf and bill_for_leasing.docx, you don’t want to end up with folder names like bills for the first and documents for the second. These results are technically valid, but they’re disconnected. We need to group related files together first, and the best way to do that is by clustering their embeddings. For messy-folder-reorganizer-ai I picked agglomerative hierarchical clustering and I will try to explain my choice to the reader. Selecting a Clustering Method There are many clustering algorithms out there, but not all are suitable for the nature of embeddings. We're working with: High-dimensional vectors (e.g., 384, 768, or more dimensions). Relatively small datasets (e.g., a few hundred or thousand files). Here's a comparison of a few clustering options: Algorithm Pros Cons K-Means Fast, simple, widely used Requires choosing k, assumes spherical clusters DBSCAN Detects arbitrary shapes, noise handling Sensitive to parameters, poor with high dimensions HDBSCAN Improved DBSCAN, handles hierarchy Slower, more complex Agglomerative No need for k, builds hierarchy, flexible distances Slower, high memory use Agglomerative hierarchical clustering is a strong fit because it: Doesn’t require you to predefine the number of clusters. Works well with custom distance metrics (like cosine). Builds a dendrogram that can be explored at different levels of granularity. Agglomerative Clustering Preparations Input: Embedding Matrix We assume an input matrix of shape M x N: M: Number of files (embeddings). N: Dimensionality of the embeddings (depends on the model used). Building a Normalized Matrix What is normalization? Normalization ensures that all vectors are of unit length, which is especially important when using cosine distance. Why normalize? Prevents length from affecting similarity. Ensures cosine distance reflects angular difference only. Formula: For vector (x), normalize it as: x̂ = x / ||x|| Where ||x|| is the Euclidean norm (i.e., the square root of the sum of squares of the elements of x). Building the Distance Matrix Using Cosine Distance Why cosine distance? It captures semantic similarity better in high-dimensional embedding spaces. More stable than Euclidean in high dimensions. Does it help with the curse of dimensionality? To some extent, yes. While no method fully escapes the curse, cosine similarity is more robust than Euclidean for textual or semantic data. Formula: Given two normalized vectors (x) and (y): cosine_similarity(x, y) = (x · y) / (‖x‖ · ‖y‖) cosine_distance(x, y) = 1 - cosine_similarity(x, y) Agglomerative Clustering Algorithm Once we have the distance matrix, the agglomerative process begins: Start: Treat each embedding as its own cluster. Merge: Find the two closest clusters using the selected linkage method: Single: Minimum distance between points across clusters. Complete: Maximum distance. Average: Mean distance. Ward: Minimizes variance (works only with Euclidean distance). Repeat: Merge the next closest pair until one cluster remains or a distance threshold is reached. Cut the dendrogram: Decide how many clusters to extract based on height (distance) or desired granularity. This method gives you interpretable, connected groupings—a critical step before folder naming or generating structured representations. Implementation If you are interested, you can check out implementation on Rust here Looking for Feedback I’d really appreciate any feedback — positive or critical — on the project, the codebase, the article series, or the general approach used in the CLI. Thanks for Reading! Feel free to reach out here or connect with me on: GitHub LinkedIn Or just drop me a note if you want to chat about Rust, AI, or creative ways to clean up messy folders!
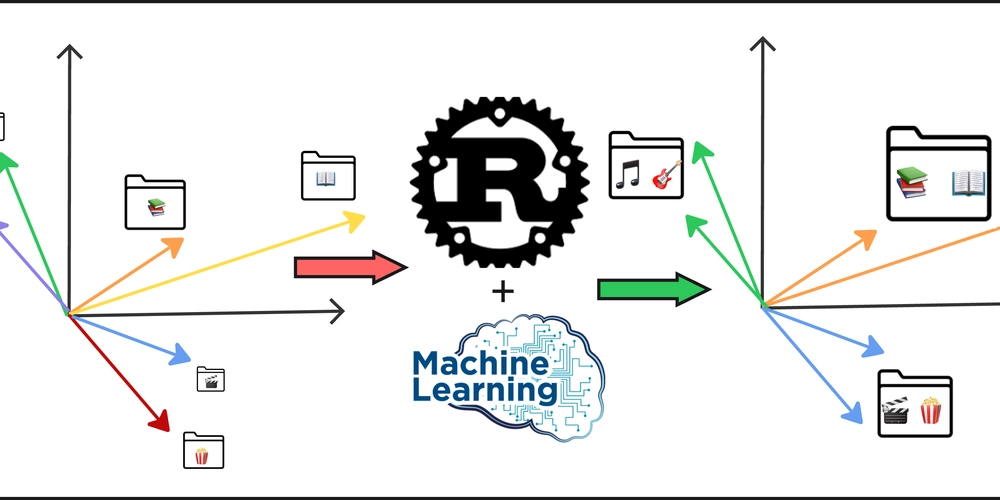
Adding RAG and ML to Messy-Folder-Reorganizer-AI
Why ML Methods for Clustering
As we discovered in previous articles, all LLMs have context restrictions, so we cannot send hundreds of file names to an LLM and ask it to create folder names for all of them. On the other hand, sending a request for each file separately is not only inefficient and redundant—it also breaks the global context.
For example, if you have files like bill_for_electricity.pdf and bill_for_leasing.docx, you don’t want to end up with folder names like bills for the first and documents for the second. These results are technically valid, but they’re disconnected. We need to group related files together first, and the best way to do that is by clustering their embeddings.
For messy-folder-reorganizer-ai I picked agglomerative hierarchical clustering and I will try to explain my choice to the reader.
Selecting a Clustering Method
There are many clustering algorithms out there, but not all are suitable for the nature of embeddings. We're working with:
- High-dimensional vectors (e.g., 384, 768, or more dimensions).
- Relatively small datasets (e.g., a few hundred or thousand files).
Here's a comparison of a few clustering options:
| Algorithm | Pros | Cons |
|---|---|---|
| K-Means | Fast, simple, widely used | Requires choosing k, assumes spherical clusters |
| DBSCAN | Detects arbitrary shapes, noise handling | Sensitive to parameters, poor with high dimensions |
| HDBSCAN | Improved DBSCAN, handles hierarchy | Slower, more complex |
| Agglomerative | No need for k, builds hierarchy, flexible distances |
Slower, high memory use |
Agglomerative hierarchical clustering is a strong fit because it:
- Doesn’t require you to predefine the number of clusters.
- Works well with custom distance metrics (like cosine).
- Builds a dendrogram that can be explored at different levels of granularity.
Agglomerative Clustering Preparations
Input: Embedding Matrix
We assume an input matrix of shape M x N:
-
M: Number of files (embeddings). -
N: Dimensionality of the embeddings (depends on the model used).
Building a Normalized Matrix
What is normalization?
Normalization ensures that all vectors are of unit length, which is especially important when using cosine distance.
Why normalize?
- Prevents length from affecting similarity.
- Ensures cosine distance reflects angular difference only.
Formula:
For vector (x), normalize it as:
x̂ = x / ||x||
Where ||x|| is the Euclidean norm (i.e., the square root of the sum of squares of the elements of x).
Building the Distance Matrix Using Cosine Distance
Why cosine distance?
- It captures semantic similarity better in high-dimensional embedding spaces.
- More stable than Euclidean in high dimensions.
Does it help with the curse of dimensionality?
To some extent, yes. While no method fully escapes the curse, cosine similarity is more robust than Euclidean for textual or semantic data.
Formula:
Given two normalized vectors (x) and (y):
cosine_similarity(x, y) = (x · y) / (‖x‖ · ‖y‖)
cosine_distance(x, y) = 1 - cosine_similarity(x, y)
Agglomerative Clustering Algorithm
Once we have the distance matrix, the agglomerative process begins:
- Start: Treat each embedding as its own cluster.
-
Merge: Find the two closest clusters using the selected linkage method:
- Single: Minimum distance between points across clusters.
- Complete: Maximum distance.
- Average: Mean distance.
- Ward: Minimizes variance (works only with Euclidean distance).
- Repeat: Merge the next closest pair until one cluster remains or a distance threshold is reached.
- Cut the dendrogram: Decide how many clusters to extract based on height (distance) or desired granularity.
This method gives you interpretable, connected groupings—a critical step before folder naming or generating structured representations.
Implementation
If you are interested, you can check out implementation on Rust
here
Looking for Feedback
I’d really appreciate any feedback — positive or critical — on the project, the codebase, the article series, or the general approach used in the CLI.
Thanks for Reading!
Feel free to reach out here or connect with me on:
Or just drop me a note if you want to chat about Rust, AI, or creative ways to clean up messy folders!









































































































































































![[The AI Show Episode 142]: ChatGPT’s New Image Generator, Studio Ghibli Craze and Backlash, Gemini 2.5, OpenAI Academy, 4o Updates, Vibe Marketing & xAI Acquires X](https://www.marketingaiinstitute.com/hubfs/ep%20142%20cover.png)

























































































































![[FREE EBOOKS] The Kubernetes Bible, The Ultimate Linux Shell Scripting Guide & Four More Best Selling Titles](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)



![From drop-out to software architect with Jason Lengstorf [Podcast #167]](https://cdn.hashnode.com/res/hashnode/image/upload/v1743796461357/f3d19cd7-e6f5-4d7c-8bfc-eb974bc8da68.png?#)







































































































.png?#)




.jpg?#)




















 (1).webp?#)











_Christophe_Coat_Alamy.jpg?#)




































































































![Rapidus in Talks With Apple as It Accelerates Toward 2nm Chip Production [Report]](https://www.iclarified.com/images/news/96937/96937/96937-640.jpg)