Big O para Desenvolvedores Java: Entenda Complexidade de Algoritmos com Exemplos Reais

O que é a Notação Big O e Por Que Deveria Me Importar? Imagine que você está tentando escolher o melhor caminho para ir ao trabalho. Você tem várias opções: carro, ônibus, trem ou a pé. O tempo que cada opção leva depende da distância, mas também de outros fatores: A pé: quanto mais longe, proporcionalmente mais tempo leva De carro: em distâncias curtas é rápido, mas em longas distâncias pode enfrentar congestionamentos De trem: tem um tempo fixo de espera, mas depois é rápido para distâncias longas A notação Big O é como um sistema para classificar esses "caminhos" (algoritmos) com base em como eles se comportam quando precisam lidar com mais informações (distâncias maiores). Em palavras simples: Big O nos diz o quanto um algoritmo vai ficar mais lento quando os dados aumentam. Importante: Big O pode se referir tanto à complexidade de tempo (quanto tempo o algoritmo leva para executar) quanto à complexidade de espaço (quanta memória o algoritmo usa). Neste artigo, focamos principalmente na complexidade de tempo, mas mencionaremos a complexidade de espaço quando relevante. Os Tipos Principais de Complexidade (Do Mais Rápido ao Mais Lento) O(1) - Complexidade Constante: "Tempo Fixo" Em linguagem simples: Não importa quanto os dados aumentem, o tempo continua o mesmo. Exemplo do dia a dia: Acender ou apagar uma luz com um interruptor. Não importa o tamanho do cômodo, a ação de apertar o interruptor leva o mesmo tempo. Exemplo em Java: public static boolean isEven(int number) { return number % 2 == 0; // Sempre uma operação, independente do número } O(log n) - Complexidade Logarítmica: "Divide e Conquista" Em linguagem simples: Quando os dados dobram, o algoritmo só precisa de um pouquinho mais de tempo. Exemplo do dia a dia: Procurar uma palavra no dicionário. Você abre no meio, decide se está antes ou depois, e elimina metade das páginas de uma vez. Exemplo em Java - Busca binária: public static int binarySearch(int[] array, int target) { int left = 0; int right = array.length - 1; while (left

Apr 17, 2025 - 15:33

Big O para Desenvolvedores Java: Entenda Complexidade de Algoritmos com Exemplos Reais

O que é a Notação Big O e Por Que Deveria Me Importar?

Imagine que você está tentando escolher o melhor caminho para ir ao trabalho. Você tem várias opções: carro, ônibus, trem ou a pé. O tempo que cada opção leva depende da distância, mas também de outros fatores:

A pé: quanto mais longe, proporcionalmente mais tempo leva
De carro: em distâncias curtas é rápido, mas em longas distâncias pode enfrentar congestionamentos
De trem: tem um tempo fixo de espera, mas depois é rápido para distâncias longas

A notação Big O é como um sistema para classificar esses "caminhos" (algoritmos) com base em como eles se comportam quando precisam lidar com mais informações (distâncias maiores).

Em palavras simples: Big O nos diz o quanto um algoritmo vai ficar mais lento quando os dados aumentam.

Importante: Big O pode se referir tanto à complexidade de tempo (quanto tempo o algoritmo leva para executar) quanto à complexidade de espaço (quanta memória o algoritmo usa). Neste artigo, focamos principalmente na complexidade de tempo, mas mencionaremos a complexidade de espaço quando relevante.

Os Tipos Principais de Complexidade (Do Mais Rápido ao Mais Lento)

O(1) - Complexidade Constante: "Tempo Fixo"

Em linguagem simples: Não importa quanto os dados aumentem, o tempo continua o mesmo.

Exemplo do dia a dia: Acender ou apagar uma luz com um interruptor. Não importa o tamanho do cômodo, a ação de apertar o interruptor leva o mesmo tempo.

Exemplo em Java:

public static boolean isEven(int number) {
    return number % 2 == 0;  // Sempre uma operação, independente do número
}

O(log n) - Complexidade Logarítmica: "Divide e Conquista"

Em linguagem simples: Quando os dados dobram, o algoritmo só precisa de um pouquinho mais de tempo.

Exemplo do dia a dia: Procurar uma palavra no dicionário. Você abre no meio, decide se está antes ou depois, e elimina metade das páginas de uma vez.

Exemplo em Java - Busca binária:

public static int binarySearch(int[] array, int target) {
    int left = 0;
    int right = array.length - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (array[mid] == target)
            return mid;  // Encontrou!

        if (array[mid] < target)
            left = mid + 1;  // Procura na metade direita
        else
            right = mid - 1;  // Procura na metade esquerda
    }

    return -1;  // Não encontrou
}

O(n) - Complexidade Linear: "Olha Tudo Uma Vez"

Em linguagem simples: O tempo aumenta na mesma proporção que os dados. Dados duas vezes maiores = tempo duas vezes maior.

Exemplo do dia a dia: Ler um livro. Se o livro tiver o dobro de páginas, vai levar aproximadamente o dobro do tempo para ler.

Exemplo em Java - Encontrar o maior valor em um array:

public static int findMax(int[] array) {
    int max = array[0];

    for (int i = 1; i < array.length; i++) {
        if (array[i] > max) {
            max = array[i];
        }
    }

    return max;
}

O(n log n) - Complexidade Linearítmica: "Dividir, Ordenar e Juntar"

Em linguagem simples: Um pouco mais lento que linear, mas muito melhor que quadrático.

Exemplo do dia a dia: Organizar cartas de baralho usando o método "dividir em montes menores, ordenar cada monte e depois juntar".

Exemplo em Java - Merge Sort (algoritmo de ordenação eficiente):

public static void mergeSort(int[] array, int left, int right) {
    if (left < right) {
        // Encontra o meio do array
        int mid = left + (right - left) / 2;

        // Ordena as duas metades
        mergeSort(array, left, mid);
        mergeSort(array, mid + 1, right);

        // Junta as metades ordenadas
        merge(array, left, mid, right);
    }
}

A função merge combina as duas metades ordenadas em uma única sequência ordenada.

O(n²) - Complexidade Quadrática: "Compara Repetidamente"

Em linguagem simples: Muito mais lento quando os dados aumentam. Dados duas vezes maiores = tempo quatro vezes maior.

Exemplo do dia a dia: Verificar se há duplicatas em uma lista comparando cada item com todos os outros.

Exemplo em Java - Bubble Sort (algoritmo de ordenação simples mas ineficiente):

public static void bubbleSort(int[] array) {
    int n = array.length;

    for (int i = 0; i < n - 1; i++) {            
        for (int j = 0; j < n - i - 1; j++) {
            if (array[j] > array[j + 1]) {
                // Troca os elementos
                int temp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = temp;
            }
        }
    }
}

O Bubble Sort compara repetidamente pares de elementos vizinhos e "borbulha" os maiores valores para o final do array em cada passada. É simples de entender, mas ineficiente para grandes conjuntos de dados.

O(2^n) - Complexidade Exponencial: "Explosão Combinatória"

Em linguagem simples: Fica absurdamente lento muito rápido. Cada elemento adicional praticamente dobra o tempo.

Exemplo do dia a dia: Tentar adivinhar uma senha testando todas as combinações possíveis.

Exemplo em Java - Calculando Fibonacci de forma recursiva ineficiente:

public static int fibonacci(int n) {
    if (n <= 1) {
        return n;
    }

    return fibonacci(n - 1) + fibonacci(n - 2);
}

Este código é extremamente ineficiente porque calcula os mesmos valores várias vezes. Para calcular fibonacci(5), ele acaba calculando fibonacci(2) três vezes!

Comparando as Velocidades

Para entender melhor o impacto dessas complexidades, vamos comparar quanto tempo (aproximadamente) cada uma levaria com diferentes tamanhos de entrada:

Complexidade	10 itens	100 itens	1000 itens
O(1)	1 segundo	1 segundo	1 segundo
O(log n)	3 segundos	7 segundos	10 segundos
O(n)	10 segundos	100 segundos	1000 segundos
O(n log n)	33 segundos	664 segundos	9970 segundos
O(n²)	100 seg	10000 seg	1000000 seg
O(2^n)	1024 seg	Muitos anos	Idade do universo

Importante: Os valores acima são apenas ilustrativos e servem para demonstrar a diferença de crescimento entre as complexidades. A notação Big O não mede tempo absoluto em segundos, e sim o comportamento relativo do algoritmo quando os dados aumentam.

Nota sobre casos: Neste artigo, estamos considerando o pior caso de complexidade para cada algoritmo, que é o cenário mais comum de análise em entrevistas e na prática. Muitos algoritmos podem ter desempenho melhor em certos cenários.

Por Que Isso É Importante Para Você

Mesmo se você está apenas começando a programar, entender o Big O te ajuda a:

Escrever programas mais rápidos: Escolher o algoritmo certo pode transformar um programa que demoraria horas em um que demora segundos.
Passar em entrevistas: Empresas de tecnologia adoram perguntar sobre Big O em entrevistas.
Entender quando seu código vai falhar: Saberá prever quando seu programa funciona bem com 100 itens mas falha com 10.000.
Fazer escolhas inteligentes: Algoritmos mais simples (como O(n²)) são mais fáceis de escrever, mas algoritmos mais eficientes (como O(n log n)) valem a pena para grandes conjuntos de dados.

Como Melhorar a Eficiência dos Seus Algoritmos

Use estruturas de dados apropriadas: Um HashMap pode transformar uma busca O(n) em O(1).
Memorize resultados intermediários: Se seu código calcula a mesma coisa várias vezes, guarde o resultado da primeira vez. Veja como podemos melhorar o Fibonacci:

public static int fibBetter(int n) {
    // Guarda resultados já calculados
    int[] memo = new int[n+1];
    return fibHelper(n, memo);
}

private static int fibHelper(int n, int[] memo) {
    if (n <= 1) return n;

    // Se já calculamos antes, só retorna o valor guardado
    if (memo[n] != 0) return memo[n];

    // Calcula e guarda para uso futuro
    memo[n] = fibHelper(n-1, memo) + fibHelper(n-2, memo);
    return memo[n];
}

Com esta técnica de memoization, o algoritmo passa de uma complexidade de O(2^n) para apenas O(n), um ganho gigantesco! Note também que criamos um array auxiliar, o que aumenta a complexidade de espaço para O(n).

Divida para conquistar: Quebre problemas grandes em problemas menores e resolva cada um separadamente.
Evite loops aninhados desnecessários: Dois loops aninhados geralmente significam O(n²).

Conclusão: Por Onde Começar?

O Big O pode parecer assustador no início, mas começar é simples:

Identifique os loops: Um único loop geralmente é O(n), loops aninhados geralmente são O(n²).
Reconheça padrões comuns: Busca binária é O(log n), algoritmos de ordenação geralmente são O(n log n) ou O(n²).
Pratique: Tente analisar o código que você já escreveu. Qual seria sua complexidade Big O?
Comece com eficiência razoável: Não se preocupe em otimizar tudo imediatamente. Comece com algo que funciona (mesmo que seja O(n²)) e melhore se for necessário.

Lembre-se: escrever um código que funciona é o primeiro passo. Fazê-lo eficiente é o segundo. O Big O te ajuda a entender quando o segundo passo é realmente necessário!

Dica Final

Se alguém lhe perguntar sobre a complexidade do seu algoritmo em uma entrevista, não tenha medo de pensar alto:

"Vejo que estou percorrendo o array uma vez, então isso é O(n)..."
"Aqui tenho dois loops aninhados, então estamos falando de O(n²)..."

Mostrar seu raciocínio é tão importante quanto chegar à resposta certa!

Para Quem Quer Saber Mais: Além do Big O

Embora o Big O seja o mais comum e o que você vai encontrar na maioria dos contextos, existem outras notações importantes:

Ω (Ômega): Representa o melhor caso (limite inferior). Por exemplo, a busca em um array pode ser O(n) no pior caso, mas é Ω(1) no melhor caso (quando o elemento está na primeira posição).
Θ (Theta): Representa quando o melhor e o pior caso coincidem. Um algoritmo é Θ(n) quando seu desempenho é sempre proporcional a n, sem variação significativa.

Na prática e em entrevistas, o foco geralmente é no Big O (pior caso) porque queremos garantir que nosso algoritmo funcione bem mesmo nas situações mais desafiadoras.

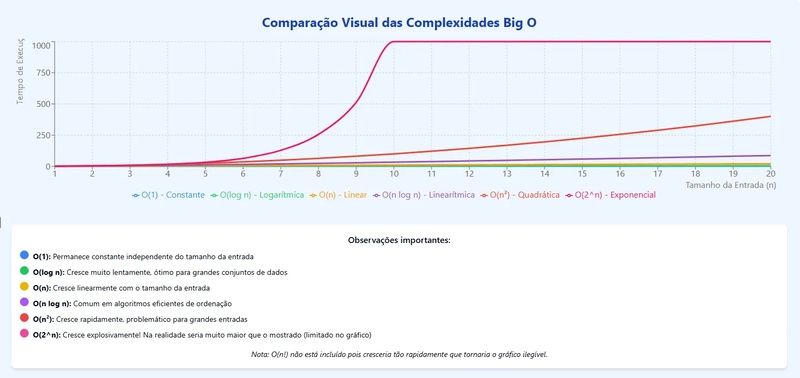
Comparação Visual das Complexidades

O gráfico acima mostra visualmente como as diferentes complexidades crescem à medida que o tamanho da entrada (n) aumenta:

O(1) permanece constante (linha horizontal azul)
O(log n) cresce muito lentamente (linha verde quase plana)
O(n) cresce de forma linear (linha amarela diagonal suave)
O(n log n) cresce um pouco mais rápido que linear (linha roxa)
O(n²) cresce rapidamente (linha vermelha subindo de forma acentuada)
O(2^n) cresce explosivamente (linha rosa quase vertical)

Observe como os algoritmos O(n²) e especialmente O(2^n) tornam-se rapidamente impraticáveis à medida que n aumenta, enquanto O(1) e O(log n) permanecem eficientes mesmo para grandes conjuntos de dados.

Referências Bibliográficas

TOSCANI, Laira Vieira; VELOSO, Paulo A. S. Complexidade de Algoritmos. Série de Livros Didáticos, Volume 13. Porto Alegre: Bookman, 2012.
BHARGAVA, Aditya Y. Entendendo Algoritmos: Um Guia Ilustrado Para Programadores e Outros Curiosos. São Paulo: Novatec Editora, 2017.
CORMEN, Thomas H.; LEISERSON, Charles E.; RIVEST, Ronald L.; STEIN, Clifford. Introduction to Algorithms. 3a ed. MIT Press, 2009.
MANZANO, José Augusto N. G.; OLIVEIRA, Jayr Figueiredo. Algoritmos: Lógica para Desenvolvimento de Programação de Computadores. 29a ed. São Paulo: Érica, 2019.
FEOFILOFF, Paulo. Algoritmos em Linguagem C. Rio de Janeiro: Elsevier/Campus, 2009.
REIS, Fábio dos. "O que é Notação Big O em programação e análise de algoritmos". Bóson Treinamentos em Ciência e Tecnologia. 24 ago. 2022. Disponível em: https://www.bosontreinamentos.com.br/estruturas-de-dados/o-que-e-notacao-big-o-em-programacao-e-analise-de-algoritmos/
BACKES, André Ricardo. Estruturas de Dados Descomplicada em Linguagem C. Rio de Janeiro: Elsevier, 2016.
SZWARCFITER, Jayme Luiz; MARKENZON, Lilian. Estruturas de Dados e seus Algoritmos. 3a ed. Rio de Janeiro: LTC, 2010.
ZIVIANI, Nivio. Projeto de Algoritmos com Implementações em Pascal e C. 3a ed. São Paulo: Cengage Learning, 2010.
SEDGEWICK, Robert; WAYNE, Kevin. Algorithms. 4a ed. Addison-Wesley Professional, 2011.