Beyond Logits: The Rise of Tribit Democracy in Language Modeling

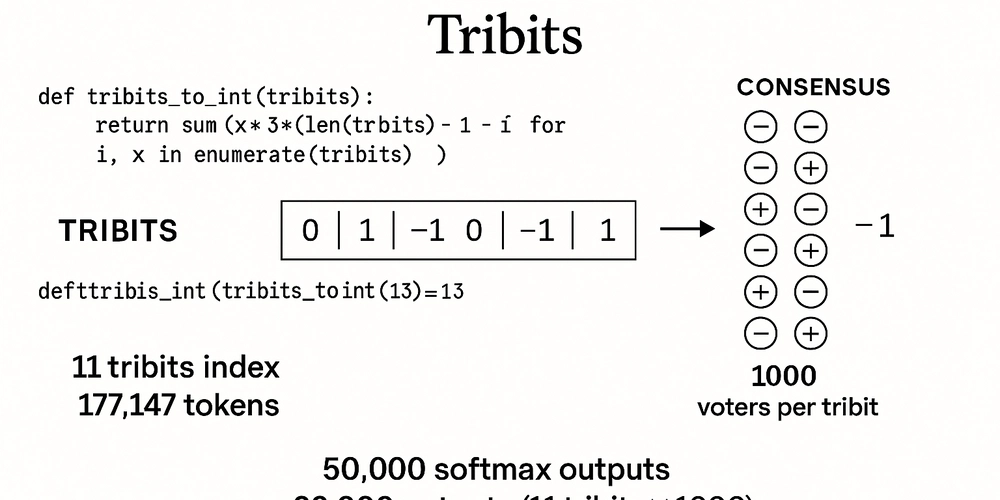
The Problem with Token Prediction Today Modern language models operate on a fundamental illusion: that token classification via a massive softmax layer is inherently optimal. In practice, this leads to bloated architectures where the final layer is forced to memorize a mapping across 50,000+ discrete classes using an argmax over logits. The size of this output layer scales linearly with the vocabulary, becoming one of the largest parameter sinks in the model. Worse, the mechanism is brittle: one misstep in logit magnitude, and the model collapses to an incorrect prediction. Tokenization itself is a coping mechanism for this architectural limitation. Byte Pair Encoding, WordPiece, and unigram tokenizers were not born out of linguistic elegance, but out of necessity. They exist to reduce vocabulary size just enough to make logit-based models computationally feasible. In essence, we have bent language to fit the convenience of a prehistoric argmax operation. Enter Tribits: A Combinatorial Perspective Instead of mapping tokens directly to individual neurons, we can reframe token prediction as address resolution. Consider the vocabulary size of GPT-2: 50,257 tokens. This fits easily within an 11-digit ternary number. Each token can be represented not as a singular output class, but as a sequence of 11 tribits (trinary digits: -1, 0, 1). This simple change redefines the output space from flat classification to compositional addressing. # Example: encoding a token ID to tribits import math def int_to_tribits(n, num_bits=11): tribits = [] while n > 0: n, rem = divmod(n, 3) if rem == 2: tribits.append(-1) n += 1 else: tribits.append(rem) while len(tribits) Tribits: [1, -1, -1, -1, 1, 0, 0, 1, 0, 0, -1] This is not just a binary substitute. It's a ternary encoding that allows vast expressiveness and error margin. With 11 tribits, we gain access to over 177,000 unique addresses. This surplus isn't waste; it's design headroom. It means that our model has tens of thousands of unused addresses it can route through, allowing for redundancy, distributed voting, and failure recovery. Why Base-3 Changes the Game Switching from binary (base-2) to ternary (base-3) increases capacity dramatically. Each additional tribit carries log3(2) ≈ 1.58 times more information than a bit. This is exponential growth: three choices per position instead of two. For comparison: 10 bits (binary) = 1024 possibilities 10 tribits (ternary) = 59,049 possibilities 11 bits (binary) = 2048 possibilities 11 tribits (ternary) = 177,147 possibilities Notice the jump: while adding one more bit only doubles the number of possibilities, adding one more tribit increases the space by a factor of three. By shifting to base-3, we move from thinking in powers of 2 to powers of 3, gaining enormous address space. This expansion allows us to encode a colossal vocabulary without resorting to crude tokenization tricks like lemmatization, stemming, or synthetic subword construction. Words, phrases, or even entire expressions could be stored directly without mutilation. Now consider a small bump: moving from 11 tribits to 12 tribits. 12 tribits (ternary) = 531,441 possibilities Over half a million unique addresses — effortlessly. This is enough to store not just every word in a language, but every inflection, neologism, slang variation, and new token ever coined, all with massive redundancy left over. No hacks, no compression tricks, no language mangling necessary. In effect, the shift to tribits reclaims the integrity of language that modern tokenizers sacrifice for computational expediency. Multiplexed Addressing and Distributed Voting Each tribit is not determined by a single neuron, but by a small committee of neurons. For instance, 10 neurons may vote on each tribit, with the average vote passed through a thresholding function to yield -1, 0, or 1. This means that the model's output isn't a monolithic softmax, but a matrix of small democracies. # Simulate voting for a tribit import torch votes = torch.tensor([1.2, 0.9, 1.1, 0.8, 1.0, -0.2, 0.7, 0.6, 1.3, 0.95]) # 10 neurons avg_vote = votes.mean() tribit = -1 if avg_vote 0.5 else 0 print("Consensus tribit:", tribit) Output: Consensus tribit: 1 This example shows how even mildly aligned neurons can result in a robust decision. Instead of betting everything on the tallest logit, we trust the collective voice of the neuron group. By scaling this structure to 110 output neurons (11 tribits x 10 neurons each), we replace a 50k-dimensional softmax layer with a compact, interpretable, and highly redundant voting system. And if 10 neurons per tribit are not enough, the model can scale further: 20, 50, even 5000 neurons per tribit, with only linear cost. Compared to the combinatorial explosion of softmax, the tribit approach is both scalable and elegant.

Apr 25, 2025 - 19:54

Beyond Logits: The Rise of Tribit Democracy in Language Modeling

The Problem with Token Prediction Today

Modern language models operate on a fundamental illusion: that token classification via a massive softmax layer is inherently optimal. In practice, this leads to bloated architectures where the final layer is forced to memorize a mapping across 50,000+ discrete classes using an argmax over logits. The size of this output layer scales linearly with the vocabulary, becoming one of the largest parameter sinks in the model. Worse, the mechanism is brittle: one misstep in logit magnitude, and the model collapses to an incorrect prediction.

Tokenization itself is a coping mechanism for this architectural limitation. Byte Pair Encoding, WordPiece, and unigram tokenizers were not born out of linguistic elegance, but out of necessity. They exist to reduce vocabulary size just enough to make logit-based models computationally feasible. In essence, we have bent language to fit the convenience of a prehistoric argmax operation.

Enter Tribits: A Combinatorial Perspective

Instead of mapping tokens directly to individual neurons, we can reframe token prediction as address resolution. Consider the vocabulary size of GPT-2: 50,257 tokens. This fits easily within an 11-digit ternary number. Each token can be represented not as a singular output class, but as a sequence of 11 tribits (trinary digits: -1, 0, 1). This simple change redefines the output space from flat classification to compositional addressing.

# Example: encoding a token ID to tribits
import math

def int_to_tribits(n, num_bits=11):
    tribits = []
    while n > 0:
        n, rem = divmod(n, 3)
        if rem == 2:
            tribits.append(-1)
            n += 1
        else:
            tribits.append(rem)
    while len(tribits) < num_bits:
        tribits.append(0)
    return tribits[::-1]

print("Token ID 15496 -> Tribits:", int_to_tribits(15496))

Output:

Token ID 15496 -> Tribits: [1, -1, -1, -1, 1, 0, 0, 1, 0, 0, -1]

This is not just a binary substitute. It's a ternary encoding that allows vast expressiveness and error margin. With 11 tribits, we gain access to over 177,000 unique addresses. This surplus isn't waste; it's design headroom. It means that our model has tens of thousands of unused addresses it can route through, allowing for redundancy, distributed voting, and failure recovery.

Why Base-3 Changes the Game

Switching from binary (base-2) to ternary (base-3) increases capacity dramatically. Each additional tribit carries log3(2) ≈ 1.58 times more information than a bit. This is exponential growth: three choices per position instead of two. For comparison:

10 bits (binary) = 1024 possibilities
10 tribits (ternary) = 59,049 possibilities
11 bits (binary) = 2048 possibilities
11 tribits (ternary) = 177,147 possibilities

Notice the jump: while adding one more bit only doubles the number of possibilities, adding one more tribit increases the space by a factor of three.

By shifting to base-3, we move from thinking in powers of 2 to powers of 3, gaining enormous address space. This expansion allows us to encode a colossal vocabulary without resorting to crude tokenization tricks like lemmatization, stemming, or synthetic subword construction. Words, phrases, or even entire expressions could be stored directly without mutilation.

Now consider a small bump: moving from 11 tribits to 12 tribits.

12 tribits (ternary) = 531,441 possibilities

Over half a million unique addresses — effortlessly.
This is enough to store not just every word in a language, but every inflection, neologism, slang variation, and new token ever coined, all with massive redundancy left over. No hacks, no compression tricks, no language mangling necessary.

In effect, the shift to tribits reclaims the integrity of language that modern tokenizers sacrifice for computational expediency.

Multiplexed Addressing and Distributed Voting

Each tribit is not determined by a single neuron, but by a small committee of neurons. For instance, 10 neurons may vote on each tribit, with the average vote passed through a thresholding function to yield -1, 0, or 1. This means that the model's output isn't a monolithic softmax, but a matrix of small democracies.

# Simulate voting for a tribit
import torch

votes = torch.tensor([1.2, 0.9, 1.1, 0.8, 1.0, -0.2, 0.7, 0.6, 1.3, 0.95])  # 10 neurons
avg_vote = votes.mean()
tribit = -1 if avg_vote < -0.5 else 1 if avg_vote > 0.5 else 0
print("Consensus tribit:", tribit)

Output:

Consensus tribit: 1

This example shows how even mildly aligned neurons can result in a robust decision. Instead of betting everything on the tallest logit, we trust the collective voice of the neuron group.

By scaling this structure to 110 output neurons (11 tribits x 10 neurons each), we replace a 50k-dimensional softmax layer with a compact, interpretable, and highly redundant voting system. And if 10 neurons per tribit are not enough, the model can scale further: 20, 50, even 5000 neurons per tribit, with only linear cost. Compared to the combinatorial explosion of softmax, the tribit approach is both scalable and elegant.

Resiliency Through Spare Capacity

The elegance of tribits lies in their surplus capacity. With so many unused addresses, models can encode not just one correct output, but neighborhoods of nearby addresses that decode to the same token. Even if a few neuron votes are corrupted, the model can still resolve to the correct output through redundancy.

To illustrate, suppose a tribit address gets minor perturbations:

true_address = [1, 0, -1, 1, 0, 0, -1, 1, 0, 0, 1]
noisy_address = [1, 0, 0, 1, 0, 0, -1, 1, 0, 0, 1]  # 1-bit noise

# Both resolve to the same token if mapped via tribits_to_int -> token

Now consider the best-case scalability: suppose each tribit is determined not by 10 neurons, but by 100 or even 1000. At 100 neurons per tribit and 11 tribits, the model uses 1,100 output neurons—still drastically smaller than a 50,000-class softmax. At 1000 neurons per tribit, the full head is 11,000 outputs—comparable to medium-sized classifiers but with far higher resiliency, interpretability, and structured fault recovery. This is not just token prediction; it's federated token governance.

This resiliency is impossible in traditional softmax architectures, where each token is a single point in logit space.

Crayon-eater ML developers continue to increase vocabulary sizes and parameter counts in pursuit of marginal gains, ignoring the fundamental flaw in the token prediction mechanism. The tribit model does not inflate capacity; it reallocates it. Instead of building ever-wider tables, it builds deeper, more fault-tolerant address systems.

Toward a Post-Softmax Language Model

The tribit approach offers a compelling alternative: smaller output heads, better interpretability, and vastly improved error tolerance. More importantly, it shifts the burden of precision away from a single max logit and distributes it across a robust council of neurons.

This is not an incremental change. It's a redefinition of what it means to "predict a token" in the first place.

A Thought Experiment to Close

Imagine redesigning the GPT-4 output head. Instead of a 130,000-class softmax demanding 130,000 logits per inference step, we employ 14 tribits (to cover more than 4 million possibilities), each governed by 100 neurons. That's only 1,400 outputs — and yet with absurd redundancy and resiliency intact.

The GPT-4 softmax layer alone demands hundreds of millions of parameters; the tribit model would demand an order of magnitude fewer. It would be smaller, faster, smoother, and virtually immune to minor inference noise.

*Even if we never reach 99% accuracy, democracy does not require it. Inference is not an oracle. If your consensus hits 50% plus one vote — it’s already winning. *

That's the threshold where neural language democracy becomes legitimate. It’s not about perfection. It’s about structured consensus outperforming brute-force confidence.

This isn't speculative fiction. It's math. It's engineering. It's reality.

And when crayon-eating ML architects realize they've been worshiping a softmax bottleneck for a decade, they'll understand that post-softmax democracy wasn't just an option.

It was inevitable.

Welcome to the post-softmax era.