781. Rabbits in Forest

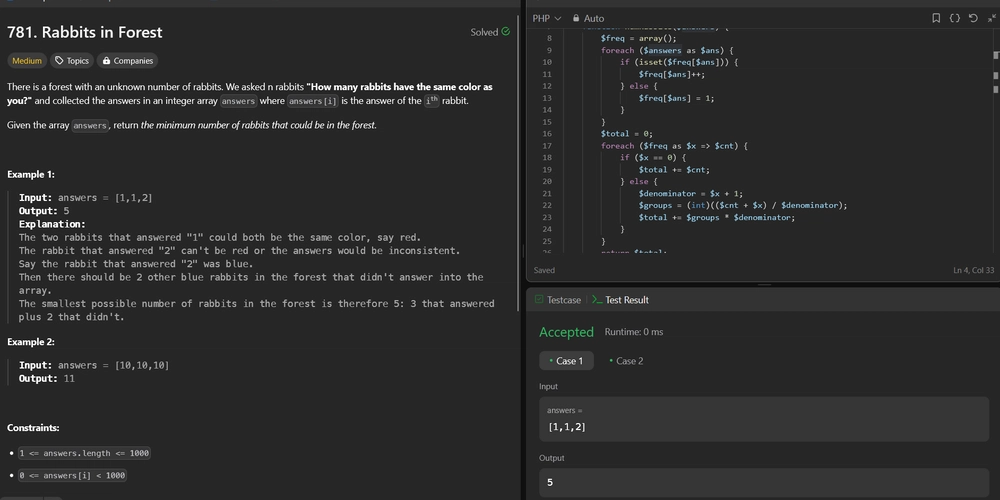
781. Rabbits in Forest Difficulty: Medium Topics: Array, Hash Table, Math, Greedy There is a forest with an unknown number of rabbits. We asked n rabbits "How many rabbits have the same color as you?" and collected the answers in an integer array answers where answers[i] is the answer of the ith rabbit. Given the array answers, return the minimum number of rabbits that could be in the forest. Example 1: Input: answers = [1,1,2] Output: 5 Explanation: The two rabbits that answered "1" could both be the same color, say red. The rabbit that answered "2" can't be red or the answers would be inconsistent. Say the rabbit that answered "2" was blue. Then there should be 2 other blue rabbits in the forest that didn't answer into the array. The smallest possible number of rabbits in the forest is therefore 5: 3 that answered plus 2 that didn't. Example 2: Input: answers = [10,10,10] Output: 11 Constraints: 1 Explanation: Frequency Count: We use a hash map to count how many times each answer appears. This helps in efficiently grouping the rabbits by their answers. Group Calculation: For each answer x (except 0), the number of groups required is calculated by the formula (count + x) // (x + 1), which ensures we round up to the nearest integer. Multiplying the number of groups by x + 1 gives the total rabbits for that answer. Handling Zero Answers: Rabbits that answer 0 must be counted individually since each such rabbit is the only one of its color. This approach efficiently computes the minimum number of rabbits by leveraging grouping based on the answers, ensuring optimal group sizes to minimize the total count. Contact Links If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks

Apr 20, 2025 - 14:29

Difficulty: Medium

Topics: Array, Hash Table, Math, Greedy

There is a forest with an unknown number of rabbits. We asked n rabbits "How many rabbits have the same color as you?" and collected the answers in an integer array answers where answers[i] is the answer of the i^th rabbit.

Given the array answers, return the minimum number of rabbits that could be in the forest.

Example 1:

Input: answers = [1,1,2]
Output: 5
Explanation:
- The two rabbits that answered "1" could both be the same color, say red.
- The rabbit that answered "2" can't be red or the answers would be inconsistent.
- Say the rabbit that answered "2" was blue.
- Then there should be 2 other blue rabbits in the forest that didn't answer into the array.
- The smallest possible number of rabbits in the forest is therefore 5: 3 that answered plus 2 that didn't.

Example 2:

Input: answers = [10,10,10]
Output: 11

Constraints:

1 <= answers.length <= 1000
0 <= answers[i] < 1000

Solution:

We need to determine the minimum number of rabbits in a forest based on the answers provided by the rabbits. Each rabbit's answer indicates how many other rabbits share the same color. Our task is to compute the minimum possible number of rabbits that could be present in the forest given these answers.

Approach

Frequency Count: First, we count the frequency of each answer using a hash map. This helps us group rabbits that gave the same answer.
Calculate Minimum Groups: For each unique answer x, we need to determine the minimum number of groups required. Each group of rabbits that answered x must have exactly x + 1 rabbits (since a rabbit answering x implies there are x other rabbits of the same color).
Summing Up: For each answer x, compute the minimum number of rabbits required using the formula to determine the number of groups and then summing up the total rabbits from all groups.

Let's implement this solution in PHP: 781. Rabbits in Forest


/**
 * @param Integer[] $answers
 * @return Integer
 */
function numRabbits($answers) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Test cases
echo numRabbits(array(1, 1, 2)) . "\n"; // Output: 5
echo numRabbits(array(10, 10, 10)) . "\n"; // Output: 11
?>

Explanation:

Frequency Count: We use a hash map to count how many times each answer appears. This helps in efficiently grouping the rabbits by their answers.
Group Calculation: For each answer x (except 0), the number of groups required is calculated by the formula (count + x) // (x + 1), which ensures we round up to the nearest integer. Multiplying the number of groups by x + 1 gives the total rabbits for that answer.
Handling Zero Answers: Rabbits that answer 0 must be counted individually since each such rabbit is the only one of its color.

This approach efficiently computes the minimum number of rabbits by leveraging grouping based on the answers, ensuring optimal group sizes to minimize the total count.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks