2999. Count the Number of Powerful Integers
2999. Count the Number of Powerful Integers Difficulty: Hard Topics: Math, String, Dynamic Programming You are given three integers start, finish, and limit. You are also given a 0-indexed string s representing a positive integer. A positive integer x is called powerful if it ends with s (in other words, s is a suffix of x) and each digit in x is at most limit. Return the total number of powerful integers in the range [start..finish]. A string x is a suffix of a string y if and only if x is a substring of y that starts from some index (including 0) in y and extends to the index y.length - 1. For example, 25 is a suffix of 5125 whereas 512 is not. Example 1: Input: start = 1, finish = 6000, limit = 4, s = "124" Output: 5 Explanation: The powerful integers in the range [1..6000] are 124, 1124, 2124, 3124, and, 4124. All these integers have each digit
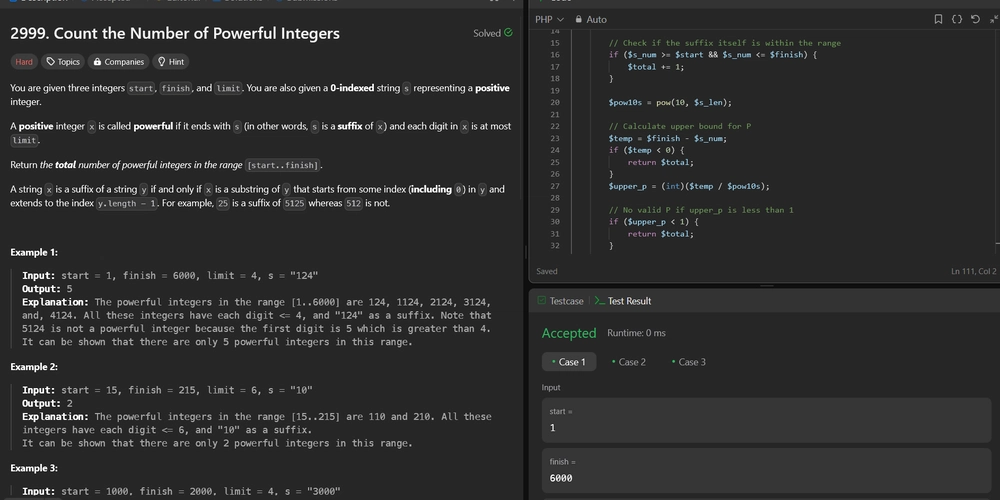
2999. Count the Number of Powerful Integers
Difficulty: Hard
Topics: Math, String, Dynamic Programming
You are given three integers start, finish, and limit. You are also given a 0-indexed string s representing a positive integer.
A positive integer x is called powerful if it ends with s (in other words, s is a suffix of x) and each digit in x is at most limit.
Return the total number of powerful integers in the range [start..finish].
A string x is a suffix of a string y if and only if x is a substring of y that starts from some index (including 0) in y and extends to the index y.length - 1. For example, 25 is a suffix of 5125 whereas 512 is not.
Example 1:
- Input: start = 1, finish = 6000, limit = 4, s = "124"
- Output: 5
-
Explanation: The powerful integers in the range [1..6000] are 124, 1124, 2124, 3124, and, 4124. All these integers have each digit <= 4, and "124" as a suffix. Note that 5124 is not a powerful integer because the first digit is 5 which is greater than 4.
- It can be shown that there are only 5 powerful integers in this range.
Example 2:
- Input: start = 15, finish = 215, limit = 6, s = "10"
- Output: 2
-
Explanation: The powerful integers in the range [15..215] are 110 and 210. All these integers have each digit <= 6, and "10" as a suffix.
- It can be shown that there are only 2 powerful integers in this range.
Example 3:
- Input: start = 1000, finish = 2000, limit = 4, s = "3000"
- Output: 0
- Explanation: All integers in the range [1000..2000] are smaller than 3000, hence "3000" cannot be a suffix of any integer in this range.
Constraints:
1 <= start <= finish <= 10151 <= limit <= 91 <= s.length <= floor(log10(finish)) + 1-
sonly consists of numeric digits which are at mostlimit. -
sdoes not have leading zeros.
Hint:
- We can use digit DP to count powerful integers in the range
[1, x]. - Let
dp[i][j]be the number of integers that haveidigits (with allowed leading 0s) andjrefers to the comparison between the current number and the prefix ofx,j == 0if the i-digit number formed currently is identical to the leftmostidigits ofx, else ifj ==1it means the i-digit number is smaller than the leftmostidigits ofx. - The answer is
count[finish] - count[start - 1], wherecount[i]refers to the number of powerful integers in the range[1..i].
Solution:
We need to count the number of powerful integers within a given range [start, finish]. A powerful integer is defined as a number that ends with a given suffix string s and all its digits are at most a given limit. The solution involves using digit dynamic programming (DP) to efficiently count valid numbers without iterating through each number in the range.
Approach
-
Check for Direct Suffix Match: First, check if the integer value of the suffix
s(denoted ass_num) lies within the range [start, finish]. If it does, this is a valid powerful integer. -
Calculate Bounds for Prefix: For numbers formed by appending
sto a prefix, compute the valid range of prefixes such that the resulting number lies within [start, finish]. The prefix must be a non-zero number with all digits ≤ limit. - Digit Dynamic Programming: Use digit DP to count valid prefixes within the computed range. This involves recursively checking each digit position while keeping track of constraints (tight bounds and leading zeros).
Let's implement this solution in PHP: 2999. Count the Number of Powerful Integers
/**
* @param Integer $start
* @param Integer $finish
* @param Integer $limit
* @param String $s
* @return Integer
*/
function numberOfPowerfulInt($start, $finish, $limit, $s) {
...
...
...
/**
* go to ./solution.php
*/
}
/**
* Helper function to count valid numbers up to X with digits <= limit and no leading zeros
*
* @param $X
* @param $limit
* @return int|mixed
*/
function count_valid($X, $limit) {
...
...
...
/**
* go to ./solution.php
*/
}
// Test Example 1
echo numberOfPowerfulInt(1, 6000, 4, "124") . "\n"; // Output: 5
// Test Example 2
echo numberOfPowerfulInt(15, 215, 6, "10") . "\n"; // Output: 2
// Test Example 3
echo numberOfPowerfulInt(1000, 2000, 4, "3000") . "\n"; // Output: 0
?>
Explanation:
-
Direct Suffix Check: Convert the suffix string
sto an integer and check if it lies within the given range. If it does, count it immediately. -
Prefix Bounds Calculation: Compute the minimum (lower_p) and maximum (upper_p) valid prefixes such that appending
sto these prefixes results in numbers within the range [start, finish]. - Digit DP for Valid Prefixes: Use a recursive helper function with memoization to count valid prefixes. The DP tracks the current digit position, whether the number being formed is still tight to the upper bound, and whether leading zeros are present. This ensures efficient counting without explicitly generating all possible numbers.
Contact Links
If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks









































































































































































![[The AI Show Episode 144]: ChatGPT’s New Memory, Shopify CEO’s Leaked “AI First” Memo, Google Cloud Next Releases, o3 and o4-mini Coming Soon & Llama 4’s Rocky Launch](https://www.marketingaiinstitute.com/hubfs/ep%20144%20cover.png)































































































































































































![Blue Archive tier list [April 2025]](https://media.pocketgamer.com/artwork/na-33404-1636469504/blue-archive-screenshot-2.jpg?#)

































.png?#)








-Baldur’s-Gate-3-The-Final-Patch---An-Animated-Short-00-03-43.png?width=1920&height=1920&fit=bounds&quality=70&format=jpg&auto=webp#)









![Apple to Split Enterprise and Western Europe Roles as VP Exits [Report]](https://www.iclarified.com/images/news/97032/97032/97032-640.jpg)























































































































![Nanoleaf Announces New Pegboard Desk Dock With Dual-Sided Lighting [Video]](https://www.iclarified.com/images/news/97030/97030/97030-640.jpg)

![Apple's Foldable iPhone May Cost Between $2100 and $2300 [Rumor]](https://www.iclarified.com/images/news/97028/97028/97028-640.jpg)