Dev.to

2444. Count Subarrays With Fixed Bounds

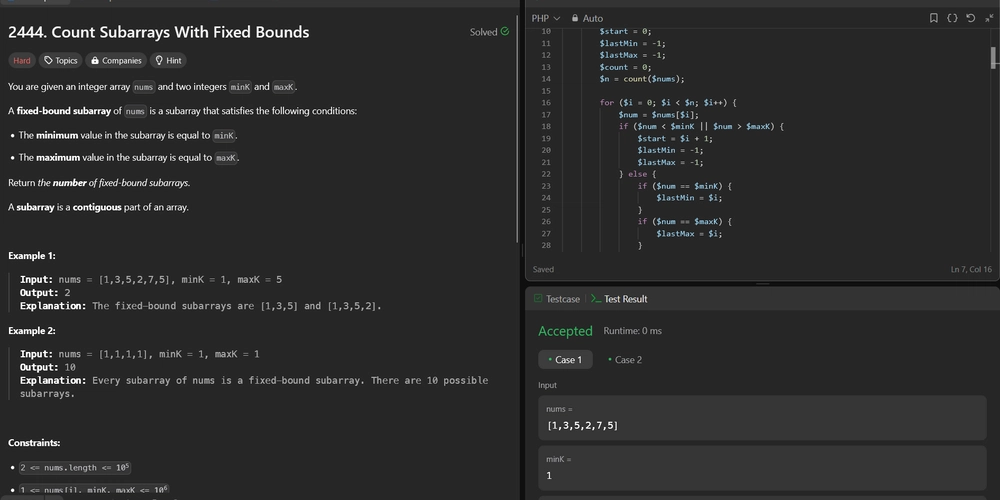
2444. Count Subarrays With Fixed Bounds Difficulty: Hard Topics: Array, Queue, Sliding Window, Monotonic Queue You are given an integer array nums and two integers minK and maxK. A fixed-bound subarray of nums is a subarray that satisfies the following conditions: The minimum value in the subarray is equal to minK. The maximum value in the subarray is equal to maxK. Return the number of fixed-bound subarrays. A subarray is a contiguous part of an array. Example 1: Input: nums = [1,3,5,2,7,5], minK = 1, maxK = 5 Output: 2 Explanation: The fixed-bound subarrays are [1,3,5] and [1,3,5,2]. Example 2: Input: nums = [1,1,1,1], minK = 1, maxK = 1 Output: 10 Explanation: Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays. Constraints: 2

Apr 26, 2025 - 14:20

Difficulty: Hard

Topics: Array, Queue, Sliding Window, Monotonic Queue

You are given an integer array nums and two integers minK and maxK.

A fixed-bound subarray of nums is a subarray that satisfies the following conditions:

The minimum value in the subarray is equal to minK.
The maximum value in the subarray is equal to maxK.

Return the number of fixed-bound subarrays.

A subarray is a contiguous part of an array.

Example 1:

Input: nums = [1,3,5,2,7,5], minK = 1, maxK = 5
Output: 2
Explanation: The fixed-bound subarrays are [1,3,5] and [1,3,5,2].

Example 2:

Input: nums = [1,1,1,1], minK = 1, maxK = 1
Output: 10
Explanation: Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays.

Constraints:

2 <= nums.length <= 10⁵
1 <= nums[i], minK, maxK <= 10⁶

Hint:

Can you solve the problem if all the numbers in the array were between minK and maxK inclusive?
Think of the inclusion-exclusion principle.
Divide the array into multiple subarrays such that each number in each subarray is between minK and maxK inclusive, solve the previous problem for each subarray, and sum all the answers.

Solution:

We need to count the number of subarrays where the minimum value is exactly minK and the maximum value is exactly maxK. These subarrays must be contiguous and all elements within them must lie between minK and maxK inclusive.

Approach

Sliding Window Technique: We maintain a sliding window where all elements are within the bounds [minK, maxK]. If an element outside these bounds is encountered, the window is reset starting from the next element.
Track Last Occurrences: For each position in the array, we keep track of the last positions where minK and maxK were encountered. This helps in determining the valid subarrays ending at each position.
Count Valid Subarrays: For each valid window, if both minK and maxK have been encountered, the number of valid subarrays ending at the current position is determined by the earliest occurrence of either minK or maxK within the window.

Let's implement this solution in PHP: 2444. Count Subarrays With Fixed Bounds


/**
 * @param Integer[] $nums
 * @param Integer $minK
 * @param Integer $maxK
 * @return Integer
 */
function countSubarrays($nums, $minK, $maxK) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example 1
$nums = array(1, 3, 5, 2, 7, 5);
$minK = 1;
$maxK = 5;
echo countSubarrays($nums, $minK, $maxK) . "\n"; // Output: 2

// Example 2
$nums = array(1, 1, 1, 1);
$minK = 1;
$maxK = 1;
echo countSubarrays($nums, $minK, $maxK) . "\n"; // Output: 10
?>

Explanation:

Sliding Window Initialization: We initialize start to 0, which marks the beginning of the current valid window. lastMin and lastMax track the last positions of minK and maxK, respectively.
Iterate Through Array: For each element in the array, check if it lies within the bounds [minK, maxK]. If not, reset the window starting from the next element and reset the last positions.
Update Last Positions: If the current element is minK or maxK, update the respective last occurrence positions.
Count Valid Subarrays: If both minK and maxK have been encountered in the current window, calculate the number of valid subarrays ending at the current position. This is determined by the earliest of the last occurrences of minK or maxK relative to the start of the window.

This approach efficiently counts the valid subarrays in linear time, ensuring optimal performance even for large input sizes.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks