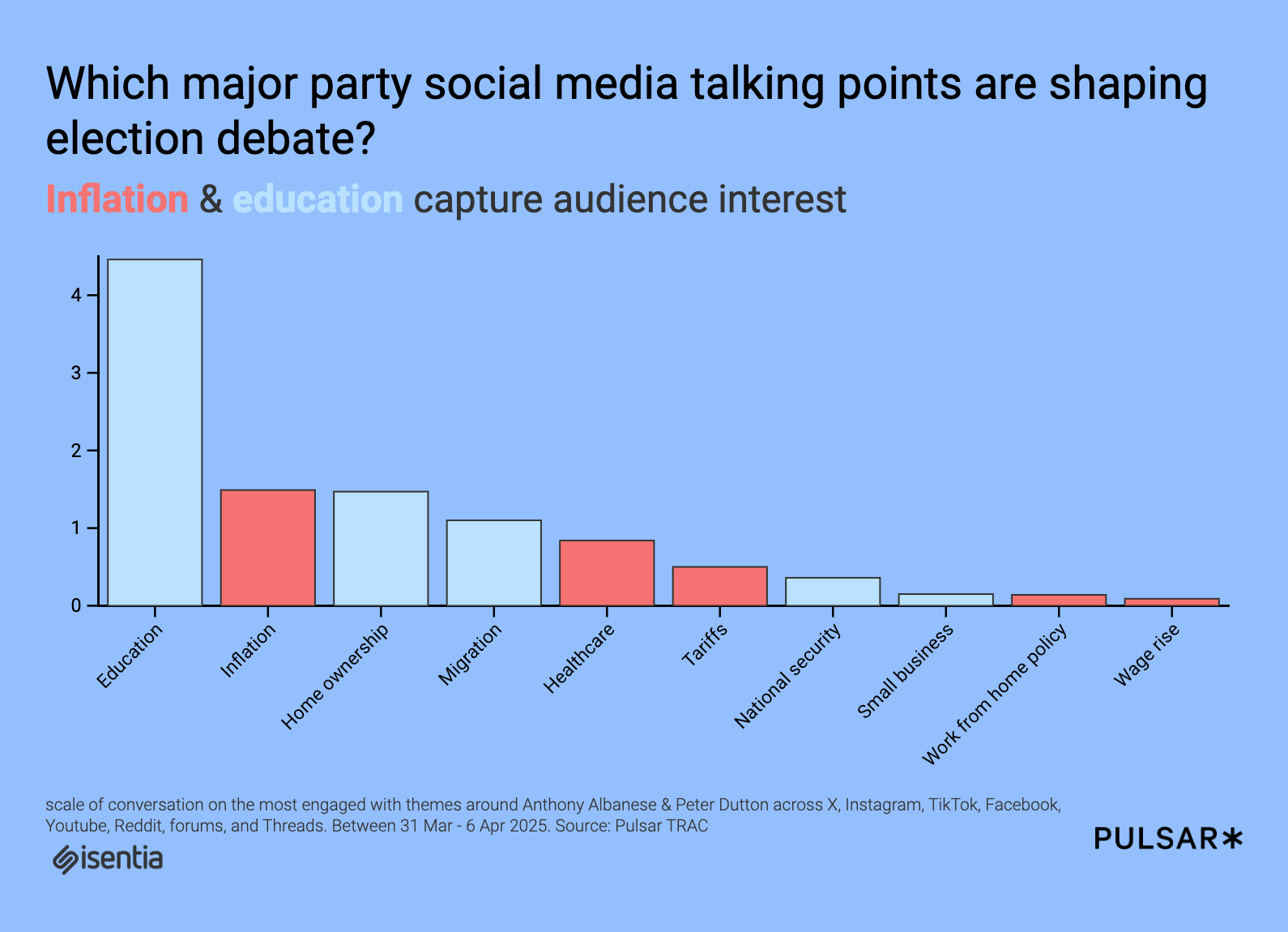
สร้าง Unsupervised Learning ด้วย K-Means Clustering โดยใช้ Python

ถ้าเรามีข้อมูลที่เราไม่รู้ว่าควรแบ่งออกเป็นกลุ่มไหน เช่น ข้อมูลลูกค้าที่ซื้อสินค้า หรือชนิดของพืชในชุดข้อมูล เราสามารถใช้ K-Means Clustering เพื่อแบ่งกลุ่มข้อมูลได้ โดยไม่ต้องมีป้ายกำกับหรือผลลัพธ์ที่รู้ล่วงหน้า ในบทความนี้ เราจะมาทำความรู้จักกับการทำ Unsupervised Learning ด้วยวิธี K-Means Clustering โดยใช้ Iris dataset ซึ่งเป็นชุดข้อมูลที่ใช้กันมากในโลกของ Machine Learning ชุดข้อมูล Iris นี้ประกอบไปด้วยข้อมูลเกี่ยวกับดอกไม้ 3 สายพันธุ์ ได้แก่ Setosa, Versicolor, และ Virginica โดยข้อมูลของแต่ละตัวอย่างจะประกอบไปด้วย 4 ลักษณะ(features) ของดอกไม้ sepal_length: ความยาวของกลีบเลี้ยง sepal_width: ความกว้างของกลีบเลี้ยง petal_length: ความยาวของกลีบปีก petal_width: ความกว้างของกลีบปีก ชุดข้อมูลนี้มีทั้งหมด 150 ตัวอย่าง ซึ่งแบ่งออกเป็น 3 กลุ่มตามชนิดของดอกไม้ และในที่นี้ เราจะใช้ K-Means Clustering เพื่อแบ่งกลุ่มข้อมูลเหล่านี้ออกเป็น 3 กลุ่มตามลักษณะของดอกไม้ที่เหมือนกัน ขั้นตอนที่ 1 นำเข้าไลบรารีและชุดข้อมูล import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline %config InlineBackend.figure_format='retina' pd.option_context('mode.use_inf_as_na', True) import warnings warnings.filterwarnings("ignore") # warnings.filterwarnings('error', category=DeprecationWarning) ขั้นตอนที่ 2 โหลดและตรวจสอบชุดข้อมูล df = pd.read_csv("https://github.com/prasertcbs/basic-dataset/raw/master/iris.csv") df.sample(5) ผลลัพธ์ที่ได้ ขั้นตอนที่ 3 นำเข้า KMeans จาก Scikit-learn from sklearn.cluster import KMeans X = df[["sepal_length", "sepal_width", "petal_length", "petal_width"]] # X = df[['petal_length', 'petal_width']] จะเลือกใช้เเค่ 2 คอลัมน์ก็ได้นะ ขั้นตอนที่ 4 ใช้Elbow Method หรือ วิธีการข้อศอก ซึ่งเป็นวิธีที่ใช้ในการหาจำนวนกลุ่ม (clusters) ที่เหมาะสมที่สุดใน KMeans clustering ssd = [] for k in range(2, 10): m = KMeans(n_clusters=k, n_init='auto') m.fit(X) ssd.append([k, m.inertia_]) ssd จะสังเกตได้ว่าค่า inertia ลดลงอย่างชัดเจนจนถึง k = 6 แล้วเริ่มลดลงช้าลงมากขึ้นใน k = 7 ถึง k = 9 ซึ่งอาจบ่งชี้ว่า k = 6 หรือประมาณนั้นอาจเป็นจำนวนกลุ่มที่เหมาะสมที่สุด ขั้นตอนที่ 5 สร้าง DataFrame เพื่อจัดระเบียบข้อมูลให้เข้าใจง่าย dd = pd.DataFrame(ssd, columns=["k", "ssd"]) dd จากผลลัพธ์ k = 3 หรือ k = 4 เป็นจำนวนกลุ่มที่เหมาะสมที่สุด เนื่องจากค่า inertia ลดลงอย่างชัดเจนที่สุดในจุดนี้ ขั้นตอนที่ 6 คำนวณเปอร์เซ็นต์การเปลี่ยนแปลงของค่า ssd dd["pct_chg"] = dd["ssd"].pct_change() * 100 dd ผลลัพธ์ที่ได้ สร้างกราฟเส้นที่เชื่อมโยงระหว่างจำนวนกลุ่ม (k) และค่า inertia (ssd) plt.plot(dd["k"], dd["ssd"], linestyle="--", marker="o") for index, row in dd.iterrows(): plt.text(row["k"] + 0.02, row["ssd"] + 0.02, f'{row["pct_chg"]:.2f}', fontsize=10) กราฟที่ได้ จากกราฟที่ได้แสดงให้เห็นว่า k = 2 ถึง k = 3: ค่า inertia ลดลงเร็ว เพราะการเพิ่มจำนวนกลุ่มช่วยให้ข้อมูลคล้ายคลึงกันมากขึ้น k = 4 ถึง k = 9: ค่า inertia ลดลงช้า เพราะการเพิ่มกลุ่มไม่ได้ช่วยทำให้ข้อมูลมีความคล้ายคลึงกันมากขึ้นเท่ากับช่วงแรก ขั้นตอนที่ 6 สร้างโมเดล KMeans ที่จะทำการ แบ่งข้อมูลออกเป็น 3 กลุ่ม ตามลักษณะของข้อมูลที่คล้ายคลึงกัน model = KMeans(n_clusters=3) model การฝึกโมเดล KMeans model.fit(X) ขั้นตอนที่ 7 การสร้าง pairplot กราฟนี้แสดงความสัมพันธ์ระหว่าง 4 คุณสมบัติของดอกไม้ (sepal_length, sepal_width, petal_length, petal_width) โดยแบ่งสีตามกลุ่ม (cluster) ที่ดอกไม้ถูกจัดให้อยู่จากการทำ KMeans clustering sns.pairplot( df, vars=["sepal_length", "sepal_width", "petal_length", "petal_width"], hue="cluster", plot_kws={"alpha": 0.4}, ) กราฟที่ได้ จุดสีแต่ละสีแสดงถึงกลุ่มต่างๆ (กลุ่ม 0, 1, 2) โดยแต่ละกลุ่มมีลักษณะการกระจายตัวของข้อมูลที่แตกต่างกัน กราฟนี้ช่วยให้เห็นความแตกต่างระหว่างแต่ละกลุ่ม (cluster) ในการกระจายของข้อมูลตามคุณลักษณะต่างๆ ตัวอย่างเพิ่มเติม เราจะลองใช้ตัวอย่างข้อมูลอื่นบ้าง เช่น ชุดข้อมูล Wine ใช้ในการจำแนกประเภทของไวน์ 3 ประเภท โดยมีคุณสมบัติที่เกี่ยวข้องกับปริมาณของสารประกอบในไวน์เช่น สี, ความเป็นกรด, ปริมาณน้ำตาล, ปริมาณแอลกอฮอล์ และสารอาหารอื่นๆ ซึ่งประกอบไปด้วย alcohol malic_acid ash alcalinity_of_ash magnesium total_phenols flavanoids nonflavanoid_phenols proanthocyanins color_intensity hue od280/od315_of_diluted_wines OD280/OD315 proline การแบ่งประเภท หรือ target มี 3 คลาส (0, 1, 2) ที่แสดงถึงประเภทของไวน์แต่ละชนิด แหล่งข้อมูล: https://archive.ics.uci.edu/ml/datasets/Wine ขั้นตอนที่ 1 นำเข้าไลบรารีและชุดข้อมูล import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline %config InlineBackend.figure_format='retina' pd.option_context('mode.use_inf_as_na', True) import warnings warnings.filterwarnings("ignore") ขั้นตอนที่ 2 โหลดและตรวจสอบชุดข้อมูล โหลด Wine dataset จาก sklearn from sklearn.datasets import load_wine data = load_wine() แปลงข้อมูลเป็น DataFrame เพิ่มคอลัมน์ 'target' ที่แสดงถึงประเภทของไวน์ (0, 1, 2) และดูข้อมูล 5 แถวแรก df = pd.DataFrame(data.data, columns=data.feature_n

Apr 11, 2025 - 17:04

สร้าง Unsupervised Learning ด้วย K-Means Clustering โดยใช้ Python

ถ้าเรามีข้อมูลที่เราไม่รู้ว่าควรแบ่งออกเป็นกลุ่มไหน เช่น ข้อมูลลูกค้าที่ซื้อสินค้า หรือชนิดของพืชในชุดข้อมูล เราสามารถใช้
K-Means Clustering เพื่อแบ่งกลุ่มข้อมูลได้ โดยไม่ต้องมีป้ายกำกับหรือผลลัพธ์ที่รู้ล่วงหน้า

ในบทความนี้ เราจะมาทำความรู้จักกับการทำ Unsupervised Learning ด้วยวิธี K-Means Clustering โดยใช้ Iris dataset ซึ่งเป็นชุดข้อมูลที่ใช้กันมากในโลกของ Machine Learning

ชุดข้อมูล Iris นี้ประกอบไปด้วยข้อมูลเกี่ยวกับดอกไม้ 3 สายพันธุ์
ได้แก่ Setosa, Versicolor, และ Virginica โดยข้อมูลของแต่ละตัวอย่างจะประกอบไปด้วย 4 ลักษณะ(features) ของดอกไม้

sepal_length: ความยาวของกลีบเลี้ยง
sepal_width: ความกว้างของกลีบเลี้ยง
petal_length: ความยาวของกลีบปีก
petal_width: ความกว้างของกลีบปีก

ชุดข้อมูลนี้มีทั้งหมด 150 ตัวอย่าง ซึ่งแบ่งออกเป็น 3 กลุ่มตามชนิดของดอกไม้ และในที่นี้ เราจะใช้ K-Means Clustering เพื่อแบ่งกลุ่มข้อมูลเหล่านี้ออกเป็น 3 กลุ่มตามลักษณะของดอกไม้ที่เหมือนกัน

ขั้นตอนที่ 1 นำเข้าไลบรารีและชุดข้อมูล

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
%config InlineBackend.figure_format='retina'

pd.option_context('mode.use_inf_as_na', True)

import warnings

warnings.filterwarnings("ignore")
# warnings.filterwarnings('error', category=DeprecationWarning)

ขั้นตอนที่ 2 โหลดและตรวจสอบชุดข้อมูล

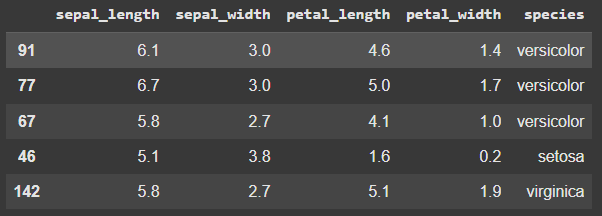
df = pd.read_csv("https://github.com/prasertcbs/basic-dataset/raw/master/iris.csv")
df.sample(5)

ผลลัพธ์ที่ได้

ขั้นตอนที่ 3 นำเข้า KMeans จาก Scikit-learn

from sklearn.cluster import KMeans     
X = df[["sepal_length", "sepal_width", "petal_length", "petal_width"]]
# X = df[['petal_length', 'petal_width']]

จะเลือกใช้เเค่ 2 คอลัมน์ก็ได้นะ

ขั้นตอนที่ 4 ใช้Elbow Method หรือ วิธีการข้อศอก

ซึ่งเป็นวิธีที่ใช้ในการหาจำนวนกลุ่ม (clusters) ที่เหมาะสมที่สุดใน KMeans clustering

ssd = []
for k in range(2, 10):
    m = KMeans(n_clusters=k, n_init='auto')
    m.fit(X)
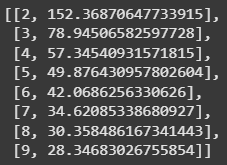
    ssd.append([k, m.inertia_])
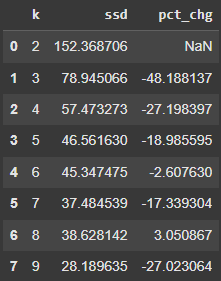
ssd

จะสังเกตได้ว่าค่า inertia ลดลงอย่างชัดเจนจนถึง k = 6 แล้วเริ่มลดลงช้าลงมากขึ้นใน k = 7 ถึง k = 9 ซึ่งอาจบ่งชี้ว่า k = 6 หรือประมาณนั้นอาจเป็นจำนวนกลุ่มที่เหมาะสมที่สุด

ขั้นตอนที่ 5 สร้าง DataFrame เพื่อจัดระเบียบข้อมูลให้เข้าใจง่าย

dd = pd.DataFrame(ssd, columns=["k", "ssd"])
dd

จากผลลัพธ์ k = 3 หรือ k = 4 เป็นจำนวนกลุ่มที่เหมาะสมที่สุด เนื่องจากค่า inertia ลดลงอย่างชัดเจนที่สุดในจุดนี้

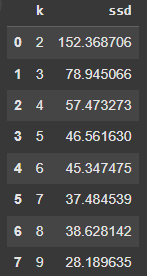
ขั้นตอนที่ 6 คำนวณเปอร์เซ็นต์การเปลี่ยนแปลงของค่า ssd

dd["pct_chg"] = dd["ssd"].pct_change() * 100
dd

ผลลัพธ์ที่ได้

สร้างกราฟเส้นที่เชื่อมโยงระหว่างจำนวนกลุ่ม (k) และค่า inertia (ssd)

plt.plot(dd["k"], dd["ssd"], linestyle="--", marker="o")

for index, row in dd.iterrows():
    plt.text(row["k"] + 0.02, row["ssd"] + 0.02, f'{row["pct_chg"]:.2f}', fontsize=10)

กราฟที่ได้

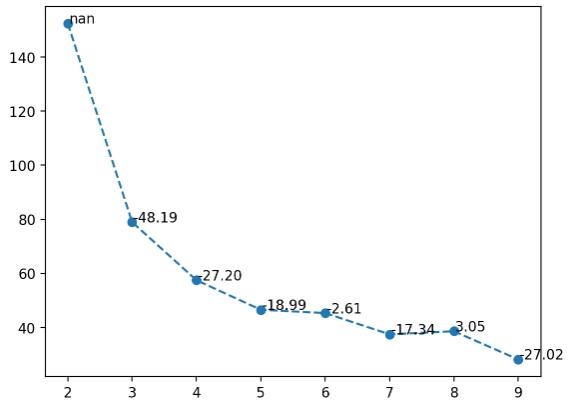
จากกราฟที่ได้แสดงให้เห็นว่า

k = 2 ถึง k = 3: ค่า inertia ลดลงเร็ว เพราะการเพิ่มจำนวนกลุ่มช่วยให้ข้อมูลคล้ายคลึงกันมากขึ้น
k = 4 ถึง k = 9: ค่า inertia ลดลงช้า เพราะการเพิ่มกลุ่มไม่ได้ช่วยทำให้ข้อมูลมีความคล้ายคลึงกันมากขึ้นเท่ากับช่วงแรก

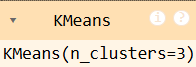
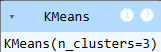
ขั้นตอนที่ 6 สร้างโมเดล KMeans ที่จะทำการ แบ่งข้อมูลออกเป็น 3 กลุ่ม ตามลักษณะของข้อมูลที่คล้ายคลึงกัน

model = KMeans(n_clusters=3)
model

การฝึกโมเดล KMeans

model.fit(X)

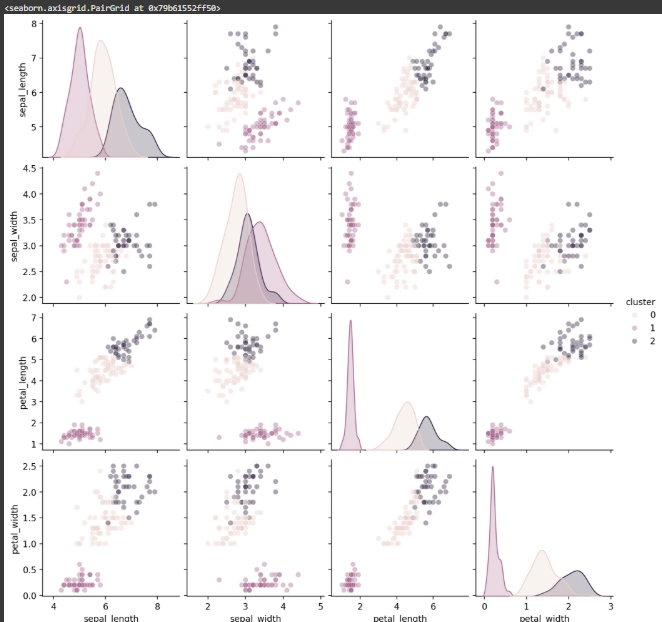
ขั้นตอนที่ 7 การสร้าง pairplot

กราฟนี้แสดงความสัมพันธ์ระหว่าง 4 คุณสมบัติของดอกไม้ (sepal_length, sepal_width, petal_length, petal_width) โดยแบ่งสีตามกลุ่ม (cluster) ที่ดอกไม้ถูกจัดให้อยู่จากการทำ KMeans clustering

sns.pairplot(
    df,
    vars=["sepal_length", "sepal_width", "petal_length", "petal_width"],
    hue="cluster",
    plot_kws={"alpha": 0.4},
)

กราฟที่ได้

จุดสีแต่ละสีแสดงถึงกลุ่มต่างๆ (กลุ่ม 0, 1, 2) โดยแต่ละกลุ่มมีลักษณะการกระจายตัวของข้อมูลที่แตกต่างกัน
กราฟนี้ช่วยให้เห็นความแตกต่างระหว่างแต่ละกลุ่ม (cluster) ในการกระจายของข้อมูลตามคุณลักษณะต่างๆ

ตัวอย่างเพิ่มเติม

เราจะลองใช้ตัวอย่างข้อมูลอื่นบ้าง เช่น ชุดข้อมูล Wine ใช้ในการจำแนกประเภทของไวน์ 3 ประเภท โดยมีคุณสมบัติที่เกี่ยวข้องกับปริมาณของสารประกอบในไวน์เช่น สี, ความเป็นกรด, ปริมาณน้ำตาล, ปริมาณแอลกอฮอล์ และสารอาหารอื่นๆ ซึ่งประกอบไปด้วย

alcohol
malic_acid
ash
alcalinity_of_ash
magnesium
total_phenols
flavanoids
nonflavanoid_phenols
proanthocyanins
color_intensity
hue
od280/od315_of_diluted_wines OD280/OD315
proline

การแบ่งประเภท หรือ target มี 3 คลาส (0, 1, 2) ที่แสดงถึงประเภทของไวน์แต่ละชนิด

แหล่งข้อมูล: https://archive.ics.uci.edu/ml/datasets/Wine

ขั้นตอนที่ 1 นำเข้าไลบรารีและชุดข้อมูล

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
%config InlineBackend.figure_format='retina'

pd.option_context('mode.use_inf_as_na', True)

import warnings

warnings.filterwarnings("ignore")

ขั้นตอนที่ 2 โหลดและตรวจสอบชุดข้อมูล

โหลด Wine dataset จาก sklearn

from sklearn.datasets import load_wine
data = load_wine()

แปลงข้อมูลเป็น DataFrame
เพิ่มคอลัมน์ 'target' ที่แสดงถึงประเภทของไวน์ (0, 1, 2) และดูข้อมูล 5 แถวแรก

df = pd.DataFrame(data.data, columns=data.feature_names)
df['target'] = data.target 
df.sample(5)

ผลลัพธ์

ขั้นตอนที่ 3 เลือกฟีเจอร์ในการทำ KMeans clustering

from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler

X = df[["alcohol", "flavanoids", "color_intensity", "proline"]]

ทำ Standardization ข้อมูล

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

ขั้นตอนที่ 4 ใช้Elbow Method หรือ วิธีการข้อศอก

ใช้ n_init=10 แทน 'auto'

ssd = []
for k in range(2, 10):
    m = KMeans(n_clusters=k, n_init=10)   
    m.fit(X_scaled)
    ssd.append([k, m.inertia_])

ssd

ผลลัพธ์ที่ได้

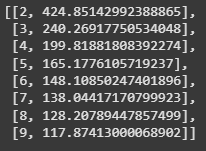
จะเห็นได้ว่าค่า inertia ลดลงเมื่อจำนวนกลุ่มเพิ่มขึ้น, แต่การลดลงจะช้าลงหลังจาก k = 5 และน้อยที่สุดที่ k = 9

ขั้นตอนที่ 5 สร้าง DataFrame เพื่อจัดระเบียบข้อมูลให้เข้าใจง่าย

dd = pd.DataFrame(ssd, columns=["k", "ssd"])
dd

ผลลัพธ์ที่ได้

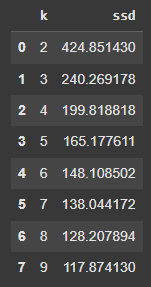
การเลือก k = 4 หรือ 5 น่าจะเป็นจำนวนกลุ่มที่เหมาะสมที่สุด เนื่องจากการลด ssd เริ่มช้าลงหลังจากนั้น

ขั้นตอนที่ 6 คำนวณเปอร์เซ็นต์การเปลี่ยนแปลงของค่า ssd

dd["pct_chg"] = dd["ssd"].pct_change() * 100
dd

ผลลัพธ์ที่ได้

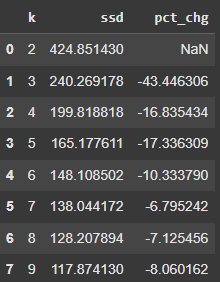
จะสังเกตได้ว่า การเพิ่มจำนวนกลุ่มทำให้ค่า ssd ลดลง แต่การลดลงเริ่มช้าลงเมื่อจำนวนกลุ่มมากขึ้น

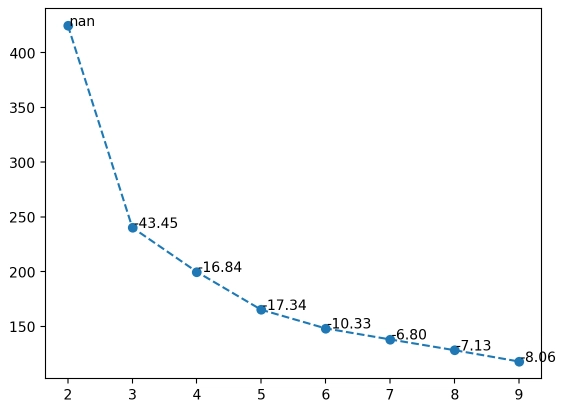
สร้างกราฟเส้นที่เชื่อมโยงระหว่างจำนวนกลุ่ม (k) และค่า inertia (ssd)

plt.plot(dd["k"], dd["ssd"], linestyle="--", marker="o")

for index, row in dd.iterrows():
    plt.text(row["k"] + 0.02, row["ssd"] + 0.02, f'{row["pct_chg"]:.2f}', fontsize=10)

ผลลัพธ์ที่ได้

ค่า ssd ลดลงอย่างมากจาก k = 2 ไป k = 3.
หลังจากนั้น การลดลงช้าลงเมื่อ k เพิ่มขึ้น.
ค่า pct_chg (เปอร์เซ็นต์การเปลี่ยนแปลง) แสดงการลดลงของ ssd ในแต่ละขั้นตอน เช่น k = 3 ลดลง 43.45%

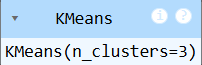
ขั้นตอนที่ 7 สร้างโมเดล KMeans ที่จะทำการ แบ่งข้อมูลออกเป็น 3 กลุ่ม ตามลักษณะของข้อมูลที่คล้ายคลึงกัน

model = KMeans(n_clusters=3)
model

การฝึกโมเดล KMeans

model.fit(X)

ขั้นตอนที่ 8 การสร้าง pairplot

sns.pairplot(
    df,
    vars=["alcohol", "flavanoids", "color_intensity", "proline"],
    hue="target",  # ใช้ target แทน cluster เพราะเราทำการจำแนกประเภทไวน์ตามกลุ่ม
    plot_kws={"alpha": 0.4},
)

กราฟที่ได้

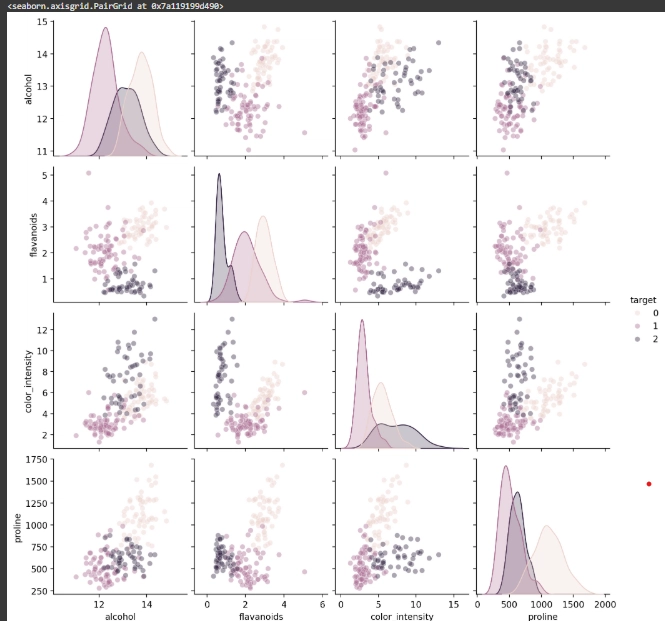
แสดงให้เห็นว่ากราฟนี้แสดงการกระจายตัวของข้อมูลไวน์ 3 ประเภท (target 0, 1, 2) ตาม 4 ฟีเจอร์: alcohol, flavanoids, color_intensity, และ proline โดยกลุ่มต่างๆ แยกออกจากกันบ้าง แต่บางกลุ่มยังทับซ้อนกันอยู่

สรุปผล
จากบทความนี้เราได้ลองใช้ K-Means Clustering เพื่อแบ่งกลุ่มข้อมูลแบบ Unsupervised Learning โดยใช้ Elbow Method เพื่อเลือกจำนวนกลุ่มที่ดีที่สุด และเรียนรู้วิธีการคำนวณ inertia เพื่อประเมินคุณภาพของการแบ่งกลุ่มอีกด้วย โดยเราจะสามารถทดลองเปลี่ยน dataset อื่นๆที่เราสนใจกันได้เองเลยนะ ลองทำดูนะคะ