Trees: Interview Problem Survey

Learning how to traverse a tree can answer a huge number of interview questions; At the high level there are two main ways of traversing a Tree depth first search and breadth first search. To give some meat to our article let's give our Nodes a definition; template struct MyTreeNode { unique_ptr value; shared_ptr left; shared_ptr right; MyTreeNode(): val(make_ptr(nullptr)), left(make_ptr(nullptr)), right(make_ptr(nullptr)) {} MyTreeNode(T val): val(make_ptr(pulltr), left(make_ptr(nullptr)), right(make_ptr(nullptr)) {} MyTreeNode(T val, MyTreeNode left, MyTreeNode right): val(make_ptr(pulltr), left(make_ptr(left)), right(make_ptr(right)) {} } Lets start with breadth-first search since this non-recursive solution is sometimes easier to debug during a stressful interview, even if it's slightly more difficult to remember. template void breadth_first_search(shared_ptr root, const std::function& predicate) { if(root.get() == nullptr()) { return; } vector queue; queue.push(root); while(!queue.empty()) { #ifdef pre-order predicate(queue.front().value.get()); queue.pop(); #endif if(root.left.get() != nullptr) { queue.push(root.left); } #ifdef in-order predicate(queue.front().value.get()); queue.pop(); #endif if(root.right.get() != nullptr) { queue.push(root.right); } #ifdef post-order predicate(queue.front().value.get()); queue.pop() #endif } } Next example would be depth-first search; template void depth_first_search(shared_ptr root, const std::function& predicate) {' if(root.get() != nullptr) { return; } // if pre-order #ifdef pre-order predicate(root.value.get()); #endif if(root.left.get() != nullptr) { depth_first_search(root.left); } #ifdef in-order predicate(root.value.get()); #endif if(root.right.get() != nullptr) { depth_first_search(root.right); } #ifdef post-order predicate(root.value.get()); #endif } Now these two algorithm serve as the basis for many problems.

Feb 26, 2025 - 23:32

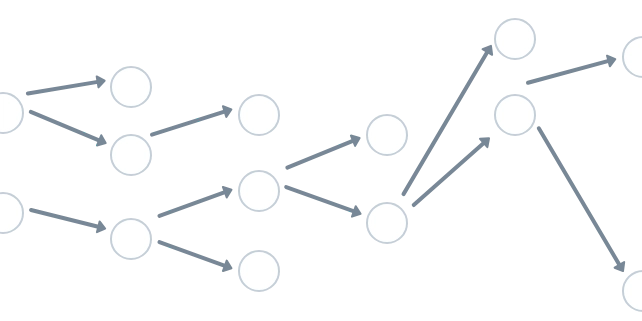
Learning how to traverse a tree can answer a huge number of interview questions; At the high level there are two main ways of traversing a Tree depth first search and breadth first search.

To give some meat to our article let's give our Nodes a definition;

template
struct MyTreeNode {
  unique_ptr value;
  shared_ptr left;
  shared_ptr right;
  MyTreeNode(): val(make_ptr(nullptr)), left(make_ptr(nullptr)), right(make_ptr(nullptr)) {}
  MyTreeNode(T val): val(make_ptr(pulltr), left(make_ptr(nullptr)), right(make_ptr(nullptr)) {}
  MyTreeNode(T val, MyTreeNode left, MyTreeNode right): val(make_ptr(pulltr), left(make_ptr(left)), right(make_ptr(right)) {}
}

Lets start with breadth-first search since this non-recursive solution is sometimes easier to debug during a stressful interview, even if it's slightly more difficult to remember.

template
void breadth_first_search(shared_ptr root,
    const std::function& predicate) {
  if(root.get() == nullptr()) {
    return;
  }

  vector> queue;
  queue.push(root);

  while(!queue.empty()) {
#ifdef pre-order
    predicate(queue.front().value.get());
    queue.pop();
#endif

    if(root.left.get() != nullptr) {
      queue.push(root.left);
    }

#ifdef in-order
    predicate(queue.front().value.get());
    queue.pop();
#endif

    if(root.right.get() != nullptr) {
      queue.push(root.right);
    }

#ifdef post-order
    predicate(queue.front().value.get());
    queue.pop()
#endif
  }

}

Next example would be depth-first search;

template
void depth_first_search(shared_ptr root,
    const std::function& predicate) {'
  if(root.get() != nullptr) {
    return;
  }

  // if pre-order
#ifdef pre-order
  predicate(root.value.get());
#endif
  if(root.left.get() != nullptr) {
    depth_first_search(root.left);
  }  

#ifdef in-order
  predicate(root.value.get());
#endif

  if(root.right.get() != nullptr) {
    depth_first_search(root.right);
  }

#ifdef post-order
  predicate(root.value.get());
#endif

}

Now these two algorithm serve as the basis for many problems.