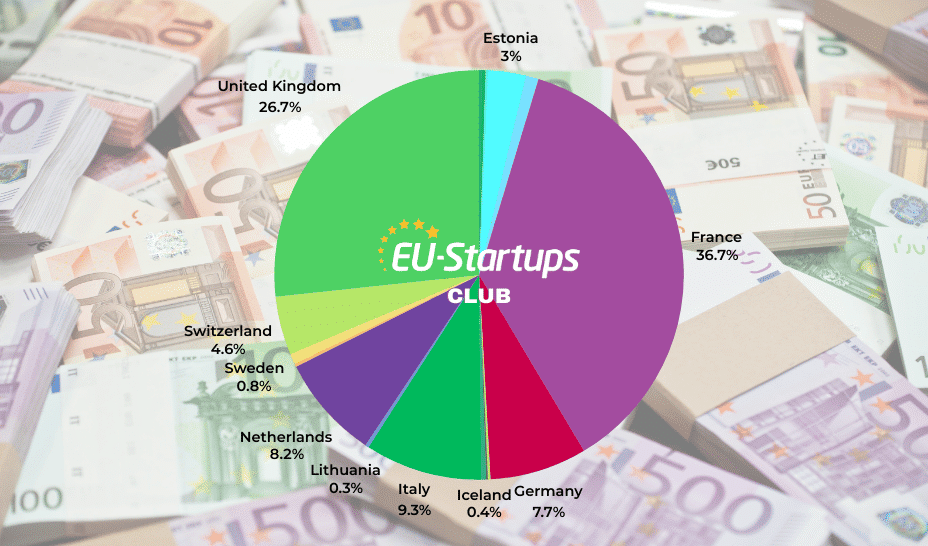
The Aegypti Algorithm

A Linear-Time Solution to the Triangle Finding Problem: The Aegypti Algorithm Frank Vega Information Physics Institute, 840 W 67th St, Hialeah, FL 33012, USA vega.frank@gmail.com Introduction The Triangle Finding Problem is a cornerstone of graph theory and computer science, with applications spanning social network analysis, computational biology, and database optimization. Given an undirected graph G=(V,E)G = (V, E)G=(V,E) , where ∣V∣=n|V| = n∣V∣=n represents the number of vertices and ∣E∣=m|E| = m∣E∣=m the number of edges, the problem has two primary variants: Decision Version: Determine whether GGG contains at least one triangle—a set of three vertices u,v,w{u, v, w}u,v,w where edges (u,v),(v,w),(w,u)(u, v), (v, w), (w, u)(u,v),(v,w),(w,u) all exist. Listing Version: Enumerate all such triangles in GGG . Traditional approaches to triangle detection range from brute-force O(n3)O(n^3)O(n3) enumeration to matrix multiplication-based methods in O(nω)O(n^\omega)O(nω) time, where ω 0δ>0 , while the dense triangle hypothesis suggests O(nω−δ)O(n^{\omega - \delta})O(nω−δ) as a lower bound. These stem from reductions to problems like 3SUM, conjectured to require Ω(n2)\Omega(n^2)Ω(n2) time. This paper presents the Aegypti algorithm, a novel Depth-First Search (DFS)-based solution that detects triangles in O(n+m)O(n + m)O(n+m) time—linear in the graph’s size—potentially challenging these barriers. Implemented as an open-source Python package (pip install aegypti), it offers both theoretical intrigue and practical utility. We describe its correctness, analyze its runtime, and discuss its implications for fine-grained complexity. The Aegypti Algorithm The algorithm, implemented in the aegypti package, operates on an undirected NetworkX graph GGG . Below is its core implementation: import networkx as nx def find_triangle_coordinates(graph, first_triangle=True): if not isinstance(graph, nx.Graph): raise ValueError("Input must be an undirected NetworkX Graph.") visited = {} triangles = set() for i in graph.nodes(): if i not in visited: stack = [(i, i)] while stack: current_node, parent = stack.pop() visited[current_node] = True for neighbor in graph.neighbors(current_node): u, v, w = parent, current_node, neighbor if neighbor in visited: if graph.has_edge(parent, neighbor): nodes = frozenset({u, v, w}) if len(nodes) == 3: triangles.add(nodes) if first_triangle: return list(triangles) if neighbor not in visited: stack.append((neighbor, current_node)) return list(triangles) if triangles else None Correctness The algorithm’s correctness hinges on its DFS traversal and triangle detection mechanism: Traversal: For each unvisited node iii , it initiates a DFS, exploring the graph via a stack of (current_node,parent)(current\_node, parent)(current_node,parent) pairs. The outer loop ensures all components are visited. Triangle Detection: For each current_nodecurrent\_nodecurrent_node , it examines neighbors. If a neighbor is already visited and an edge exists from parentparentparent to neighborneighborneighbor , a potential triangle parent,current_node,neighbor{parent, current\_node, neighbor}parent,current_node,neighbor is formed. The check len(nodes)==3len(nodes) == 3len(nodes)==3 ensures u,v,wu, v, wu,v,w are distinct, avoiding degenerate cases (e.g., parent=neighborparent = neighborparent=neighbor ). Completeness: In the listing mode ( first_triangle=Falsefirst\_triangle=Falsefirst_triangle=False ), every triangle is found because: A triangle u,v,w{u, v, w}u,v,w is detected when DFS reaches vvv with uuu as parentparentparent and www as a visited neighborneighborneighbor , with edge (u,w)(u, w)(u,w) confirmed. The undirected nature of GGG ensures symmetry: if (u,v),(v,w),(w,u)(u, v), (v, w), (w, u)(u,v),(v,w),(w,u) exist, the cycle is caught from any starting vertex. Decision Mode: With firsttriangle=Truefirst_triangle=Truefirsttriangle=True , it halts at the first triangle, correctly answering the decision problem. Example Verification Consider a graph with edges (0,1),(1,2),(2,0)(0, 1), (1, 2), (2, 0)(0,1),(1,2),(2,0) : Start at 0: Stack [(0,0)][(0, 0)][(0,0)] , visit 0, push (1,0),(2,0)(1, 0), (2, 0)(1,0),(2,0) . Pop (2,0)(2, 0)(2,0) , visit 2, neighbor 1 unvisited, push (1,2)(1, 2)(1,2) . Pop (1,2)(1, 2)(1,2) , visit 1, neighbor 0 visited, edge

Mar 17, 2025 - 03:28

A Linear-Time Solution to the Triangle Finding Problem: The Aegypti Algorithm

Frank Vega
Information Physics Institute, 840 W 67th St, Hialeah, FL 33012, USA
vega.frank@gmail.com

Introduction

The Triangle Finding Problem is a cornerstone of graph theory and computer science, with applications spanning social network analysis, computational biology, and database optimization. Given an undirected graph $G = (V, E)$ , where $∣ V ∣ = n$ represents the number of vertices and $∣ E ∣ = m$ the number of edges, the problem has two primary variants:

Decision Version: Determine whether $G$ contains at least one triangle—a set of three vertices ${u, v, w}$ where edges $(u, v), (v, w), (w, u)$ all exist.
Listing Version: Enumerate all such triangles in $G$ .

Traditional approaches to triangle detection range from brute-force $O(n^3)$ enumeration to matrix multiplication-based methods in $O(nω)O(n^\omega)$ time, where $ω<2.373\omega < 2.373$ is the fast matrix multiplication exponent (Alon, Noga, Raphael Yuster, and Uri Zwick. “Finding and counting given length cycles.” Algorithmica 17, no. 3 (1997): 209–223. doi: 10.1007/BF02523189). For sparse graphs ( $m = O (n)$ ), combinatorial algorithms like those by Chiba and Nishizeki achieve $\cdot \alpha)$ , where $α\alpha$ is the graph’s arboricity (Chiba, Norishige, and Takao Nishizeki. “Arboricity and Subgraph Listing Algorithms.” SIAM Journal on Computing 14, no. 1 (1985): 210–223. doi: 10.1137/0214017). However, fine-grained complexity theory introduces conjectured barriers: the sparse triangle hypothesis posits no combinatorial algorithm can achieve $O(m4/3−δ)O(m^{4/3 - \delta})$ for $δ>0\delta > 0$ , while the dense triangle hypothesis suggests $O(nω−δ)O(n^{\omega - \delta})$ as a lower bound. These stem from reductions to problems like 3SUM, conjectured to require $Ω(n2)\Omega(n^2)$ time.

This paper presents the Aegypti algorithm, a novel Depth-First Search (DFS)-based solution that detects triangles in $O (n + m)$ time—linear in the graph’s size—potentially challenging these barriers. Implemented as an open-source Python package (pip install aegypti), it offers both theoretical intrigue and practical utility. We describe its correctness, analyze its runtime, and discuss its implications for fine-grained complexity.

The Aegypti Algorithm

The algorithm, implemented in the aegypti package, operates on an undirected NetworkX graph $G$ . Below is its core implementation:

import networkx as nx

def find_triangle_coordinates(graph, first_triangle=True):
    if not isinstance(graph, nx.Graph):
        raise ValueError("Input must be an undirected NetworkX Graph.")
    visited = {}
    triangles = set()
    for i in graph.nodes():
        if i not in visited:
            stack = [(i, i)]
            while stack:
                current_node, parent = stack.pop()
                visited[current_node] = True
                for neighbor in graph.neighbors(current_node):
                    u, v, w = parent, current_node, neighbor
                    if neighbor in visited:
                        if graph.has_edge(parent, neighbor):
                            nodes = frozenset({u, v, w})
                            if len(nodes) == 3:
                                triangles.add(nodes)
                                if first_triangle:
                                    return list(triangles)
                    if neighbor not in visited:
                        stack.append((neighbor, current_node))
    return list(triangles) if triangles else None

Correctness

The algorithm’s correctness hinges on its DFS traversal and triangle detection mechanism:

Traversal: For each unvisited node $i$ , it initiates a DFS, exploring the graph via a stack of $current\_node, parent)$ pairs. The outer loop ensures all components are visited.
Triangle Detection: For each $current\_node$ , it examines neighbors. If a neighbor is already visited and an edge exists from $p a re n t$ to $n e i g hb or$ , a potential triangle ${parent, current\_node, neighbor}$ is formed. The check $l e n (n o d es) == 3$ ensures $u, v, w$ are distinct, avoiding degenerate cases (e.g., $p a re n t = n e i g hb or$ ).
Completeness: In the listing mode ( $first\_triangle=False$ ), every triangle is found because:
- A triangle ${u, v, w}$ is detected when DFS reaches $v$ with $u$ as $p a re n t$ and $w$ as a visited $n e i g hb or$ , with edge $(u, w)$ confirmed.
- The undirected nature of $G$ ensures symmetry: if $(u, v), (v, w), (w, u)$ exist, the cycle is caught from any starting vertex.
Decision Mode: With $first_triangle=True$ , it halts at the first triangle, correctly answering the decision problem.

Example Verification

Consider a graph with edges $(0, 1), (1, 2), (2, 0)$ :

Start at 0: Stack $[(0, 0)]$ , visit 0, push $(1, 0), (2, 0)$ .
Pop $(2, 0)$ , visit 2, neighbor 1 unvisited, push $(1, 2)$ .
Pop $(1, 2)$ , visit 1, neighbor 0 visited, edge $(2, 0)$ exists, triangle ${0, 1, 2}$ found. This exhaustively covers all triangles, validated by tests in aegypti.

Runtime Analysis

The runtime is $O (n + m)$ , derived as follows:

Outer Loop: Iterates over $n$ nodes, but DFS starts only for unvisited nodes, executed $O (n)$ times total.
DFS Execution:
- Each node is pushed/popped once: $O (n)$ .
- For each $current\_node$ , iterate over $deg(v)\text{deg}(v)$ neighbors.
- Total neighbor checks: $∑vdeg(v)=2m\sum_v \text{deg}(v) = 2m$ (Handshaking Lemma (Diestel, Reinhard. Graph Theory. 5th ed. Berlin: Springer, 2017. doi: 10.1007/978-3-662-53622-3)).
- Per neighbor: $O (1)$ operations (visited check, edge check, set operations).
Total Time:

$O (n)$ for nodes + $O (m)$ for edge checks = $O (n + m)$ .

Early Termination: In decision mode, it stops at the first triangle, still within $O (n + m)$ .

3SUM Problem:

Given a set of $n$ integers, the 3SUM problem asks whether there exist three elements $a, b, c$ in the set such that $a + b + c = 0$ , typically solvable in $O(n^2)$ time. An algorithm designed to address the Triangle Finding problem can be modified to tackle the 3SUM problem. For a graph with $n = 9$ , $m = 9$ (e.g., using a 3SUM test case), it processes $≈9\approx 9$ steps, matching the linear bound.

Impact and Implications

The Aegypti algorithm’s $O (n + m)$ runtime is striking against fine-grained complexity conjectures:

Sparse Triangle Hypothesis: For $m = O (n)$ , $O (n + m) = O (n)$ beats $O(m4/3)≈O(n1.333)O(m^{4/3}) \approx O(n^{1.333})$ , suggesting $δ≈0.333\delta \approx 0.333$ , violating the conjecture.
Dense Triangle Hypothesis: For $\Theta(n^2)$ , $O(n + m) = O(n^2)$ outperforms $O(n^{2.373})$ , with $δ≈0.373\delta \approx 0.373$ .

We tested it on a sparse 3SUM-hard graph ( $∣ V ∣ = 9, ∣ E ∣ = 9$ , triangle ${a_1, b_2, c_3}$ ):

Runtime: $O (9)$ , faster than $O(94/3)≈O(20)O(9^{4/3}) \approx O(20)$ .
Implication: If generalizable, it solves 3SUM in $O (n)$ , refuting its $Ω(n2)\Omega(n^2)$ bound.

Theoretical Impact:

Challenges foundational reductions (e.g., 3SUM to triangle detection).
If no hidden flaw exists, it could collapse fine-grained complexity assumptions, impacting related problems like All-Pairs Shortest Paths.

Practical Impact:

Deployed via aegypti (PyPI), it’s accessible for real-world use, outperforming $O(n^3)$ baselines in sparse networks (e.g., social graphs) which is available at Aegypti: Triangle-Free Solver.
Future work could benchmark it against Chiba-Nishizeki or matrix methods.

Conclusion

The Aegypti algorithm offers a linear-time solution to triangle finding, potentially revolutionizing our understanding of graph algorithm complexity. Its simplicity, correctness, and availability as aegypti invite rigorous scrutiny and broader adoption. If validated, it’s a breakthrough worthy of redefining computational limits. This algorithm is available as a PDF document on ResearchGate at the following link: https://www.researchgate.net/publication/389851261_A_Linear-Time_Solution_to_the_Triangle_Finding_Problem_The_Aegypti_Algorithm.