Breaking Down tanh into Its Constituent Operations (As Explained By Karpathy)

Hi there! I'm Shrijith Venkatrama, founder of Hexmos. Right now, I’m building LiveAPI, a tool that makes generating API docs from your code ridiculously easy. Breaking down tanh into its constituent operations We have the definition of tanh as follows: We can see that the above formula has: exponentiation subtraction addition division What the Value class cannot do now a = Value(2.0) a + 1 The above doesn't work, because a is of Value type whereas 1 is of int type. We can fix this by automatically trying to convert 1 into a Value type in the add method: class Value: ... def add(self, other): other = other if isinstance(other, Value) else Value(other) # convert non-Value type to Value type out = Value(self.data + other.data, (self, other), '+') Now, the following code works: a = Value(3.0) a + 1 # Gives out `Value(data=4.0)` The same line is added to mul as well to provide that automatic type conversion: other = other if isinstance(other, Value) else Value(other) Now, the following will work: a = Value(3.0) a * 2 # will give out `Value(data=6.0)` A (Potentially) Surprising Bug How about the following code - will this work? a = Value(3.0) 2 * a The answer is that - no, that doesn't work: So, to solve the ordering problem, in python we must specify rmul (right multiply): class Value: .... def rmul(self, other): # other * self return self * other Now, the following will work: Implementing The Exponential Function We add the following method for calculating exponents in the Value class. def exp(self): x = self.data out = Value(math.exp(x), (self,), 'exp') def _backward(): self.grad += out.data * out.grad # d(e^x) = e^x. Then apply chain rule out._backward = _backward return out Adding Support for a / b We want to support division of Value objects. And it happens that we can reformulate a / b in a more convenient way: a / b = a * (1 / b) = a * (b-1) To implement the above scheme we will require a pow (power) method: def pow(self, other): assert isinstance(other, (int, float)), "only supporting int/float powers for now" out = Value(self.dataother, (self,), f'**{other}') def _backward(): self.grad += (other * self.data**(other-1)) * out.grad out._backward = _backward return out The above method implements the power rule to calculate the derivative of a power expression: We also need subtraction and we do it using addition and negation: def neg(self): # -self return self * -1 def sub(self, other): # self - other return self + (-other) The Test - Replace old tanh with its constituent formula The code: # inputs x1, x2 x1 = Value(2.0, label='x1') x2 = Value(0.0, label='x2') # weights w1, w2 w1 = Value(-3.0, label='w1') w2 = Value(1.0, label='w2') # bias of the neuron b = Value(6.8813735870195432, label='b') # x1w1 + x2w2 + b x1w1 = x1 * w1; x1w1.label = 'x1w1' x2w2 = x2 w2; x2w2.label = 'x2w2' x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label = 'x1w1 + x2w2' n = x1w1x2w2 + b; n.label = 'n' # e = (2n).exp() o = (e - 1) / (e + 1) o.label = 'o' o.backward() draw_dot(o) The result: You can check via the lat post, that the output/result of the tanh operation was 0.7071. Even after the change it is the same. So looks like we were able to break down tanh into more fundamental operations such as exp, pow subtract, etc Reference The spelled-out intro to neural networks and backpropagation: building micrograd - YouTube

Feb 20, 2025 - 12:15

Hi there! I'm Shrijith Venkatrama, founder of Hexmos. Right now, I’m building LiveAPI, a tool that makes generating API docs from your code ridiculously easy.

Breaking down `tanh` into its constituent operations

We have the definition of tanh as follows:

We can see that the above formula has:

exponentiation
subtraction
addition
division

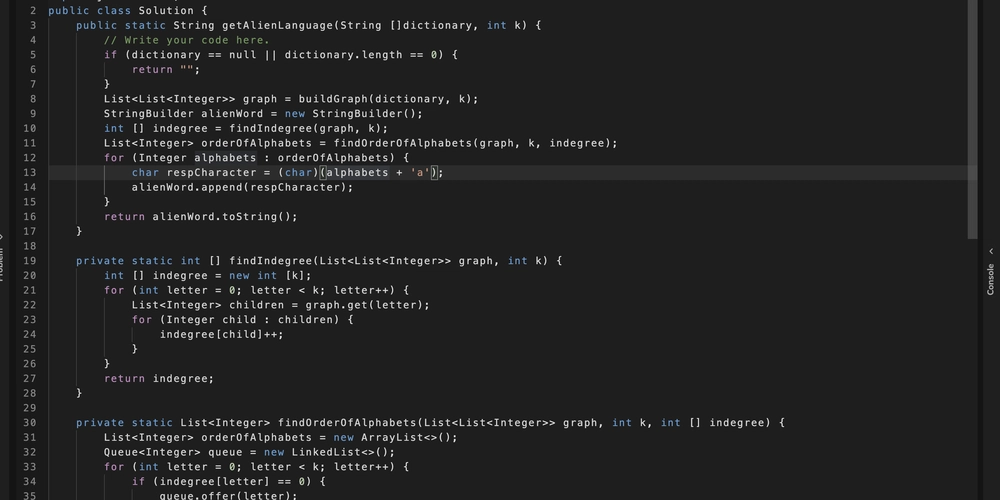
What the `Value` class cannot do now

a = Value(2.0)
a + 1

The above doesn't work, because a is of Value type whereas 1 is of int type.

We can fix this by automatically trying to convert 1 into a Value type in the __add__ method:

class Value:
    ...

    def __add__(self, other):
        other = other if isinstance(other, Value) else Value(other) # convert non-Value type to Value type
        out = Value(self.data + other.data, (self, other), '+')

Now, the following code works:

a = Value(3.0)
a + 1 # Gives out `Value(data=4.0)`

The same line is added to __mul__ as well to provide that automatic type conversion:

other = other if isinstance(other, Value) else Value(other)

Now, the following will work:

a = Value(3.0)
a * 2 # will give out `Value(data=6.0)`

A (Potentially) Surprising Bug

How about the following code - will this work?

a = Value(3.0)
2 * a

The answer is that - no, that doesn't work:

So, to solve the ordering problem, in python we must specify __rmul__ (right multiply):

class Value:
    ....
    def __rmul__(self, other): # other * self
        return self * other

Now, the following will work:

Implementing The Exponential Function

We add the following method for calculating exponents in the Value class.

  def exp(self):
    x = self.data
    out = Value(math.exp(x), (self,), 'exp')

    def _backward():
        self.grad += out.data * out.grad # d(e^x) = e^x. Then apply chain rule
    out._backward = _backward

    return out

Adding Support for `a / b`

We want to support division of Value objects. And it happens that we can reformulate a / b in a more convenient way:

a / b
= a * (1 / b)
= a * (b**-1)

To implement the above scheme we will require a pow (power) method:

    def __pow__(self, other):
        assert isinstance(other, (int, float)), "only supporting int/float powers for now"
        out = Value(self.data**other, (self,), f'**{other}')

        def _backward():
            self.grad += (other * self.data**(other-1)) * out.grad
        out._backward = _backward
        return out

The above method implements the power rule to calculate the derivative of a power expression:

We also need subtraction and we do it using addition and negation:


  def __neg__(self):  # -self
      return self * -1

  def __sub__(self, other):  # self - other
      return self + (-other)

The Test - Replace old `tanh` with its constituent formula

The code:

# inputs x1, x2
x1 = Value(2.0, label='x1')
x2 = Value(0.0, label='x2')

# weights w1, w2
w1 = Value(-3.0, label='w1')
w2 = Value(1.0, label='w2')

# bias of the neuron
b = Value(6.8813735870195432, label='b')

# x1*w1 + x2*w2 + b
x1w1 = x1 * w1; x1w1.label = 'x1*w1'
x2w2 = x2 * w2; x2w2.label = 'x2*w2'
x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label = 'x1*w1 + x2*w2'
n = x1w1x2w2 + b; n.label = 'n'

# 
e = (2*n).exp()
o = (e - 1) / (e + 1)

o.label = 'o'
o.backward()
draw_dot(o)

The result:

You can check via the lat post, that the output/result of the tanh operation was 0.7071. Even after the change it is the same. So looks like we were able to break down tanh into more fundamental operations such as exp, pow subtract, etc

Reference

The spelled-out intro to neural networks and backpropagation: building micrograd - YouTube