Big-O en Español - Parte 3
Este es el tercer post de una serie de 5 sobre la notación Big-O. En este artículo, exploraremos las expresiones logarítmicas, exponenciales y factoriales. ¿Qué encontrarás en esta serie? Parte 1: Expresiones Lineales y Constantes Introducción a las notaciones más simples y cómo afectan el rendimiento de nuestros algoritmos. Parte 2: Expresiones Cuadráticas, Cúbicas y de Otras Potencias Un análisis más profundo sobre cómo crecen los tiempos de ejecución en algoritmos más complejos. Parte 3: Expresiones Logarítmicas, Exponenciales y Factoriales Exploraremos casos donde el tiempo de ejecución crece de forma mucho más drástica. Parte 4: Combinando Complejidades y Comparando Estructuras de Datos Analizaremos cómo diferentes estructuras de datos afectan la complejidad y cómo combinar varios algoritmos. Parte 5: Consideraciones Avanzadas y Casos Reales Reflexiones finales sobre trade-offs entre tiempo y espacio, complejidades amortizadas, y cómo aplicar Big-O en escenarios reales. Expresiones Logarítmicas Un ejemplo clásico de una expresión logarítmica es la búsqueda binaria, uno de los primeros algoritmos que aprendemos en estructuras de datos. Este método requiere un arreglo ordenado para funcionar. Ejemplo de arreglo: const vector = [3, 6, 7, 12, 15, 16, 24, 25, 32, 35, 39]; Explicación Supongamos que queremos buscar el número 7. En la búsqueda binaria: Dividimos el arreglo por la mitad. Comparamos el número buscado con el valor en la posición central. Si el número buscado es menor, seguimos con la mitad izquierda; si es mayor, usamos la mitad derecha. Resultado: El número 7 está en el arreglo. Si buscamos el número 34, aplicamos la misma técnica, pero el número no se encontrará después de iterar. Código de Búsqueda Binaria function busquedaBinaria(arregloNumeros, numEncontrar) { let izquierda = 0; let derecha = arregloNumeros.length - 1; while (izquierda
Este es el tercer post de una serie de 5 sobre la notación Big-O. En este artículo, exploraremos las expresiones logarítmicas, exponenciales y factoriales.
¿Qué encontrarás en esta serie?
Parte 1: Expresiones Lineales y Constantes
Introducción a las notaciones más simples y cómo afectan el rendimiento de nuestros algoritmos.Parte 2: Expresiones Cuadráticas, Cúbicas y de Otras Potencias
Un análisis más profundo sobre cómo crecen los tiempos de ejecución en algoritmos más complejos.Parte 3: Expresiones Logarítmicas, Exponenciales y Factoriales
Exploraremos casos donde el tiempo de ejecución crece de forma mucho más drástica.Parte 4: Combinando Complejidades y Comparando Estructuras de Datos
Analizaremos cómo diferentes estructuras de datos afectan la complejidad y cómo combinar varios algoritmos.Parte 5: Consideraciones Avanzadas y Casos Reales
Reflexiones finales sobre trade-offs entre tiempo y espacio, complejidades amortizadas, y cómo aplicar Big-O en escenarios reales.
Expresiones Logarítmicas
Un ejemplo clásico de una expresión logarítmica es la búsqueda binaria, uno de los primeros algoritmos que aprendemos en estructuras de datos. Este método requiere un arreglo ordenado para funcionar.
Ejemplo de arreglo:
const vector = [3, 6, 7, 12, 15, 16, 24, 25, 32, 35, 39];
Explicación
Supongamos que queremos buscar el número 7. En la búsqueda binaria:
- Dividimos el arreglo por la mitad.
- Comparamos el número buscado con el valor en la posición central.
- Si el número buscado es menor, seguimos con la mitad izquierda; si es mayor, usamos la mitad derecha.
Resultado: El número 7 está en el arreglo.
Si buscamos el número 34, aplicamos la misma técnica, pero el número no se encontrará después de iterar.
Código de Búsqueda Binaria
function busquedaBinaria(arregloNumeros, numEncontrar) {
let izquierda = 0;
let derecha = arregloNumeros.length - 1;
while (izquierda <= derecha) {
const medio = Math.floor((izquierda + derecha) / 2);
if (arregloNumeros[medio] === numEncontrar) return medio;
if (numEncontrar < arregloNumeros[medio]) derecha = medio - 1;
else izquierda = medio + 1;
}
return -1; // Número no encontrado
}
Complejidad Matemática
La búsqueda binaria es eficiente porque no revisa todos los elementos, sino que divide el arreglo iterativamente. Matemáticamente, se representa como:
f(x) = Log x
En notación Big-O:
O(Log n)
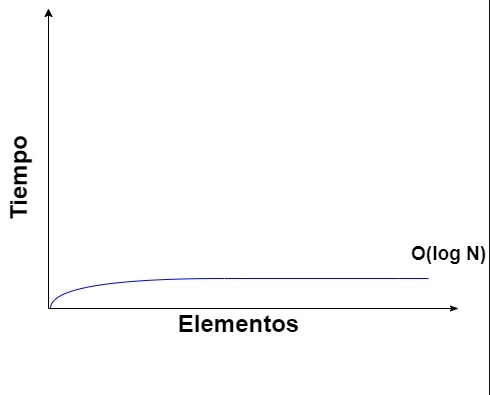
Gráfica
La gráfica de estas expresiones es:
Expresiones Exponenciales
Un ejemplo típico de una expresión exponencial es el cálculo recursivo de la serie de Fibonacci.
Fórmula de Fibonacci
F(n) = F(n-1) + F(n-2)
Código
var serieFibonacci = function(numero) {
if (numero <= 1) return numero;
return serieFibonacci(numero - 2) + serieFibonacci(numero - 1);
};
Este algoritmo calcula la serie recursivamente y, debido a que realiza muchas llamadas repetidas, es muy ineficiente para valores altos de n.
Complejidad Matemática
Matemáticamente, se representa como:
f(x) = 2^x
En notación Big-O:
O(2^n)
Gráfica
La gráfica para este tipo de expresiones es:
Expresiones Factoriales
Las expresiones factoriales son las de mayor complejidad y se observan en algoritmos que prueban todas las combinaciones posibles, como los ataques de fuerza bruta.
Ejemplo: Ataques de Fuerza Bruta
Imagina que queremos adivinar una contraseña probando todas las combinaciones de letras y números. Este enfoque es ineficiente y puede tardar días, semanas o meses dependiendo de la longitud de la contraseña.
Aunque los ataques de fuerza bruta son ineficientes, en ocasiones se diseñan algoritmos similares para explorar combinaciones donde el tiempo no es una restricción crítica.
Complejidad Matemática
Matemáticamente, se representa como:
f(x) = x!
En notación Big-O:
O(n!)
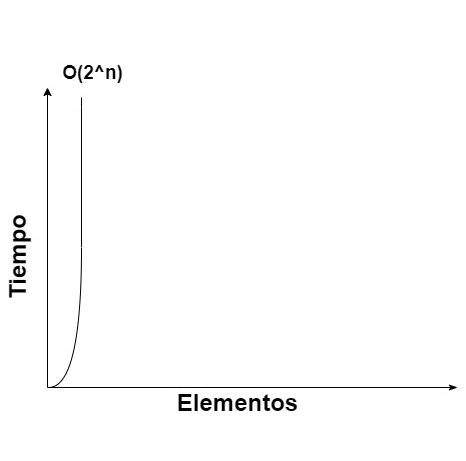
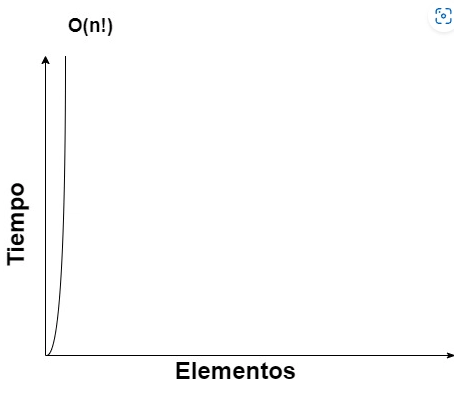
Gráfica
La gráfica de este tipo de algoritmos muestra un crecimiento extremadamente rápido:
Conclusión
En este post, hemos explorado:
- Expresiones logarítmicas (búsqueda binaria): O(Log n)
- Expresiones exponenciales (Fibonacci recursivo): O(2^n)
- Expresiones factoriales (ataques de fuerza bruta): O(n!)
En la próxima y última parte, exploraremos técnicas para optimizar algoritmos y evitar complejidades altas. ¡No te lo pierdas!





































































































































































![[The AI Show Episode 142]: ChatGPT’s New Image Generator, Studio Ghibli Craze and Backlash, Gemini 2.5, OpenAI Academy, 4o Updates, Vibe Marketing & xAI Acquires X](https://www.marketingaiinstitute.com/hubfs/ep%20142%20cover.png)














































































































![[FREE EBOOKS] The Kubernetes Bible, The Ultimate Linux Shell Scripting Guide & Four More Best Selling Titles](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)



![From drop-out to software architect with Jason Lengstorf [Podcast #167]](https://cdn.hashnode.com/res/hashnode/image/upload/v1743796461357/f3d19cd7-e6f5-4d7c-8bfc-eb974bc8da68.png?#)

































































































.png?#)




.jpg?#)





























_Christophe_Coat_Alamy.jpg?#)

































































































![Rapidus in Talks With Apple as It Accelerates Toward 2nm Chip Production [Report]](https://www.iclarified.com/images/news/96937/96937/96937-640.jpg)