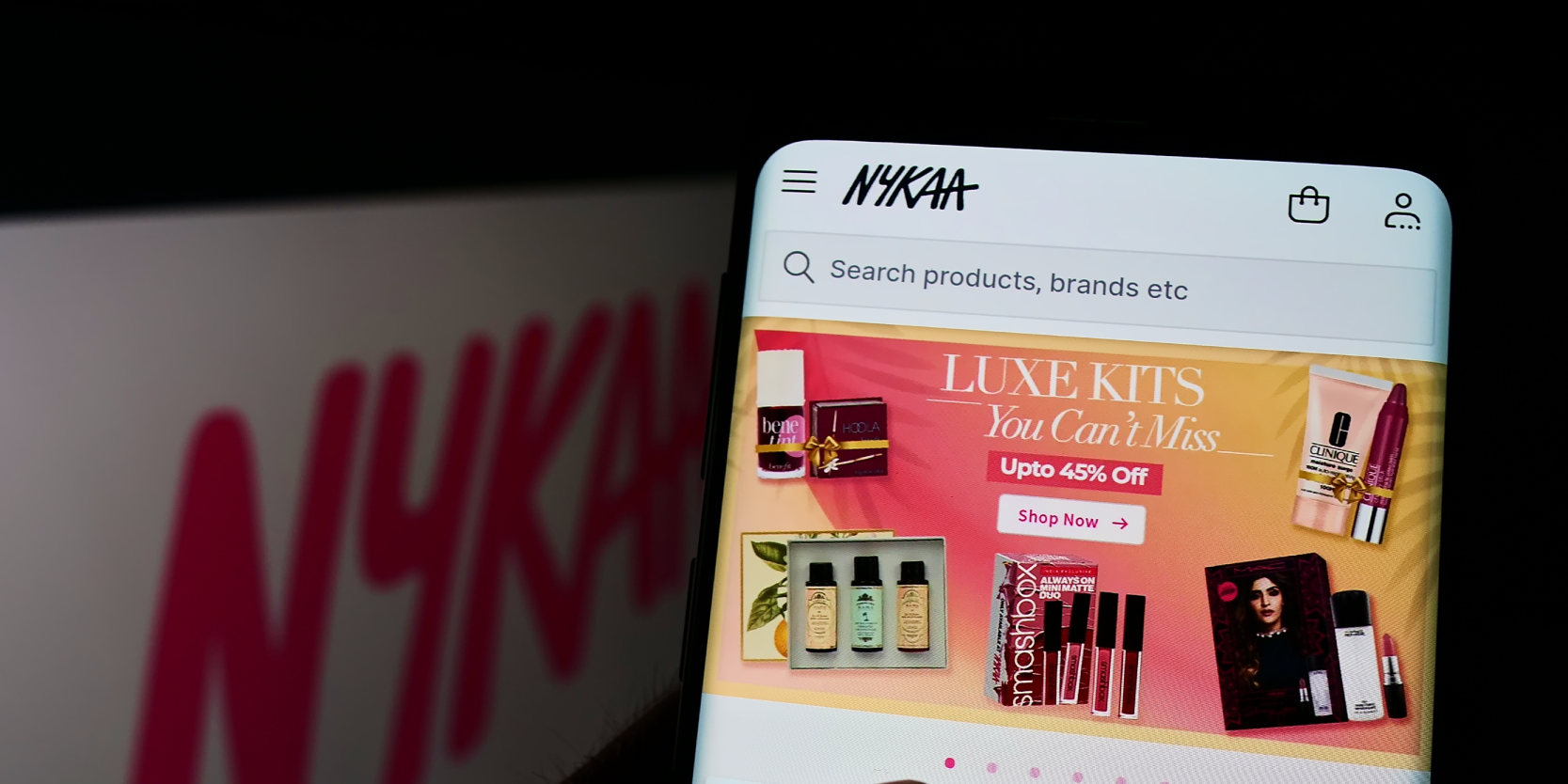
368. Largest Divisible Subset
368. Largest Divisible Subset Difficulty: Medium Topics: Array, Math, Dynamic Programming, Sorting Given a set of distinct positive integers nums, return the largest subset answer such that every pair (answer[i], answer[j]) of elements in this subset satisfies: answer[i] % answer[j] == 0, or answer[j] % answer[i] == 0 If there are multiple solutions, return any of them. Example 1: Input: nums = [1,2,3] Output: [1,2] Explanation: [1,3] is also accepted. Example 2: Input: nums = [1,2,4,8] Output: [1,2,4,8] Constraints: 1
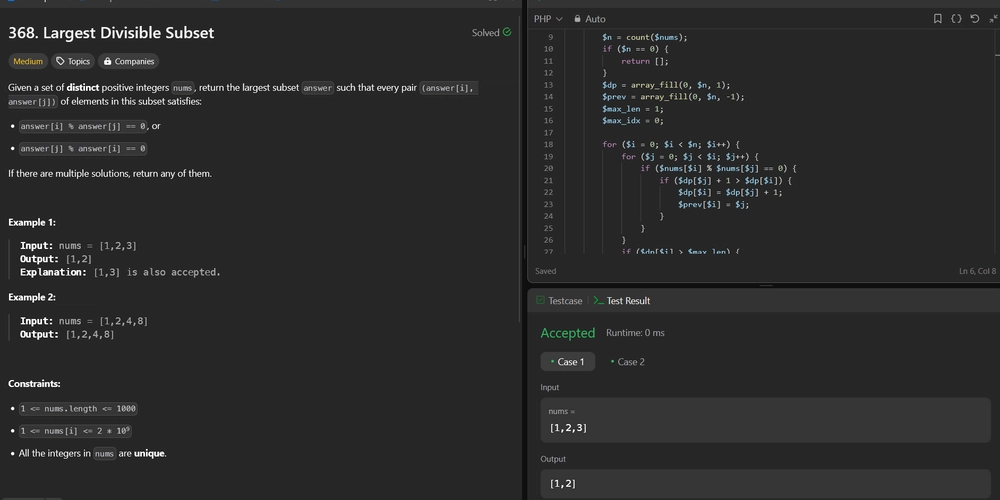
368. Largest Divisible Subset
Difficulty: Medium
Topics: Array, Math, Dynamic Programming, Sorting
Given a set of distinct positive integers nums, return the largest subset answer such that every pair (answer[i], answer[j]) of elements in this subset satisfies:
-
answer[i] % answer[j] == 0, or answer[j] % answer[i] == 0
If there are multiple solutions, return any of them.
Example 1:
- Input: nums = [1,2,3]
- Output: [1,2]
- Explanation: [1,3] is also accepted.
Example 2:
- Input: nums = [1,2,4,8]
- Output: [1,2,4,8]
Constraints:
1 <= nums.length <= 10001 <= nums[i] <= 2 * 109- All the integers in
numsare unique.
Solution:
We need to find the largest subset of distinct positive integers such that every pair of elements in the subset satisfies the divisibility condition (i.e., one element divides the other). The approach involves dynamic programming (DP) to efficiently determine the longest chain of elements where each subsequent element is a multiple of the previous one.
Approach
- Sort the Array: Sorting helps in ensuring that if we are considering elements in ascending order, each subsequent element can only be a multiple of the previous elements.
-
Dynamic Programming Setup: Use two arrays:
-
dp[i]to store the length of the largest divisible subset ending with the element at indexi. -
prev[i]to track the index of the previous element in the subset to reconstruct the answer.
-
-
DP Transition: For each element at index
i, check all previous elements at indicesj(wherej < i). If the current element is divisible by the previous element and extending the subset ending atjresults in a larger subset, updatedp[i]andprev[i]. -
Reconstruct the Subset: After filling the DP arrays, backtrack from the element with the maximum subset length to construct the result subset using the
prevarray.
Let's implement this solution in PHP: 368. Largest Divisible Subset
/**
* @param Integer[] $nums
* @return Integer[]
*/
function largestDivisibleSubset($nums) {
...
...
...
/**
* go to ./solution.php
*/
}
// Example usage:
$nums1 = [1, 2, 3];
print_r(largestDivisibleSubset($nums1)); // Possible outputs: [1,2] or [1,3]
$nums2 = [1, 2, 4, 8];
print_r(largestDivisibleSubset($nums2)); // Output: [1, 2, 4, 8]
?>
Explanation:
- Sorting: The input array is sorted in ascending order to facilitate checking divisibility in a sequential manner.
-
DP Initialization: Arrays
dpandprevare initialized to track the length of subsets and their previous elements, respectively. - DP Transition: For each element, we check all previous elements to see if they can form a valid divisible subset. If so, we update the DP values accordingly.
-
Result Construction: The maximum length subset is identified, and the subset is reconstructed by backtracking from the element with the maximum length using the
prevarray.
This approach efficiently finds the largest divisible subset using dynamic programming and backtracking, ensuring optimal performance with a time complexity of O(n2), which is feasible given the problem constraints.
Contact Links
If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks










































































































































































![[The AI Show Episode 142]: ChatGPT’s New Image Generator, Studio Ghibli Craze and Backlash, Gemini 2.5, OpenAI Academy, 4o Updates, Vibe Marketing & xAI Acquires X](https://www.marketingaiinstitute.com/hubfs/ep%20142%20cover.png)



























































































































![[DEALS] The Premium Learn to Code Certification Bundle (97% off) & Other Deals Up To 98% Off – Offers End Soon!](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)


![From drop-out to software architect with Jason Lengstorf [Podcast #167]](https://cdn.hashnode.com/res/hashnode/image/upload/v1743796461357/f3d19cd7-e6f5-4d7c-8bfc-eb974bc8da68.png?#)








































































































.png?#)

































_Christophe_Coat_Alamy.jpg?#)
 (1).webp?#)



































































































![Apple Considers Delaying Smart Home Hub Until 2026 [Gurman]](https://www.iclarified.com/images/news/96946/96946/96946-640.jpg)
![iPhone 17 Pro Won't Feature Two-Toned Back [Gurman]](https://www.iclarified.com/images/news/96944/96944/96944-640.jpg)
![Tariffs Threaten Apple's $999 iPhone Price Point in the U.S. [Gurman]](https://www.iclarified.com/images/news/96943/96943/96943-640.jpg)