2537. Count the Number of Good Subarrays
2537. Count the Number of Good Subarrays Difficulty: Medium Topics: Array, Hash Table, Sliding Window Given an integer array nums and an integer k, return the number of good subarrays of nums. A subarray arr is good if there are at least k pairs of indices (i, j) such that i < j and arr[i] == arr[j]. A subarray is a contiguous non-empty sequence of elements within an array. Example 1: Input: nums = [1,1,1,1,1], k = 10 Output: 1 Explanation: The only good subarray is the array nums itself. Example 2: Input: nums = [3,1,4,3,2,2,4], k = 2 Output: 4 Explanation: There are 4 different good subarrays: [3,1,4,3,2,2] that has 2 pairs. [3,1,4,3,2,2,4] that has 3 pairs. [1,4,3,2,2,4] that has 2 pairs. [4,3,2,2,4] that has 2 pairs. Constraints: 1
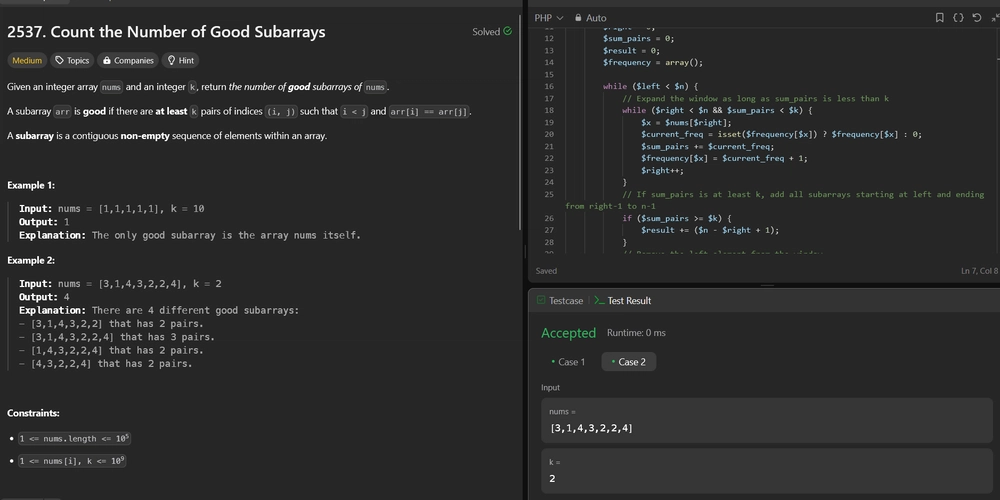
2537. Count the Number of Good Subarrays
Difficulty: Medium
Topics: Array, Hash Table, Sliding Window
Given an integer array nums and an integer k, return the number of good subarrays of nums.
A subarray arr is good if there are at least k pairs of indices (i, j) such that i < j and arr[i] == arr[j].
A subarray is a contiguous non-empty sequence of elements within an array.
Example 1:
- Input: nums = [1,1,1,1,1], k = 10
- Output: 1
- Explanation: The only good subarray is the array nums itself.
Example 2:
- Input: nums = [3,1,4,3,2,2,4], k = 2
- Output: 4
-
Explanation: There are 4 different good subarrays:
- [3,1,4,3,2,2] that has 2 pairs.
- [3,1,4,3,2,2,4] that has 3 pairs.
- [1,4,3,2,2,4] that has 2 pairs.
- [4,3,2,2,4] that has 2 pairs.
Constraints:
1 <= nums.length <= 1051 <= nums[i], k <= 109
Hint:
- For a fixed index l, try to find the minimum value of index r, such that the subarray is not good
- When a number is added to a subarray, it increases the number of pairs by its previous appearances.
- When a number is removed from the subarray, it decreases the number of pairs by its remaining appearances.
- Maintain 2-pointers l and r such that we can keep in account the number of equal pairs.
Solution:
We need to count the number of good subarrays in a given array. A good subarray is defined as one where there are at least k pairs of indices (i, j) such that i < j and arr[i] == arr[j].
Approach
The approach to solve this problem efficiently involves using a sliding window technique combined with a hash map to track the frequency of elements within the current window. Here are the key steps:
-
Sliding Window Technique: Maintain a window using two pointers,
leftandright, to explore all possible subarrays. - Frequency Tracking: Use a hash map to keep track of the frequency of each element within the current window. This helps in efficiently calculating the number of pairs contributed by each element.
- Sum of Pairs Calculation: For each element added to the window, the number of pairs increases by the current frequency of that element before it was added. Similarly, when an element is removed from the window, the number of pairs decreases by the new frequency of that element after removal.
-
Expand and Shrink Window: Expand the window by moving the
rightpointer to include more elements until the number of pairs meets or exceedsk. Once the condition is met, count all valid subarrays ending at the currentrightpointer and shrink the window by moving theleftpointer to find smaller valid subarrays.
Let's implement this solution in PHP: 2537. Count the Number of Good Subarrays
/**
* @param Integer[] $nums
* @param Integer $k
* @return Integer
*/
function countGood($nums, $k) {
...
...
...
/**
* go to ./solution.php
*/
}
// Example 1
$nums1 = array(1,1,1,1,1);
$k1 = 10;
echo countGood($nums1, $k1) . "\n"; // Output: 1
// Example 2
$nums2 = array(3,1,4,3,2,2,4);
$k2 = 2;
echo countGood($nums2, $k2) . "\n"; // Output: 4
?>
Explanation:
-
Initialization: Initialize pointers
leftandrightat the start of the array, a hash mapfrequencyto track element frequencies,sum_pairsto track the number of valid pairs, andresultto accumulate the count of good subarrays. -
Expand Window: Move the
rightpointer to expand the window. For each new element added, update its frequency and adjustsum_pairsby adding the previous frequency of that element (since each existing occurrence forms a new pair). -
Count Valid Subarrays: Once the window contains enough pairs (sum_pairs >= k), all subarrays starting from the current
leftto the currentright(and beyond) are valid. Add the count of these valid subarrays toresult. -
Shrink Window: Move the
leftpointer to shrink the window, adjusting the frequency andsum_pairsaccordingly. This ensures that we explore all possible valid subarrays starting from each position.
This approach efficiently counts all valid subarrays in linear time, O(n), by ensuring each element is processed at most twice (once added and once removed from the window).
Contact Links
If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks









































































































































































![[The AI Show Episode 144]: ChatGPT’s New Memory, Shopify CEO’s Leaked “AI First” Memo, Google Cloud Next Releases, o3 and o4-mini Coming Soon & Llama 4’s Rocky Launch](https://www.marketingaiinstitute.com/hubfs/ep%20144%20cover.png)













































































































![[DEALS] The All-in-One Microsoft Office Pro 2019 for Windows: Lifetime License + Windows 11 Pro Bundle (89% off) & Other Deals Up To 98% Off](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)


































![Is this too much for a modular monolith system? [closed]](https://i.sstatic.net/pYL1nsfg.png)


















































































































_Andreas_Prott_Alamy.jpg?width=1280&auto=webp&quality=80&disable=upscale#)



























































































![What features do you get with Gemini Advanced? [April 2025]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2024/02/gemini-advanced-cover.jpg?resize=1200%2C628&quality=82&strip=all&ssl=1)













![Apple Shares Official Trailer for 'Long Way Home' Starring Ewan McGregor and Charley Boorman [Video]](https://www.iclarified.com/images/news/97069/97069/97069-640.jpg)
![Apple Watch Series 10 Back On Sale for $299! [Lowest Price Ever]](https://www.iclarified.com/images/news/96657/96657/96657-640.jpg)
![EU Postpones Apple App Store Fines Amid Tariff Negotiations [Report]](https://www.iclarified.com/images/news/97068/97068/97068-640.jpg)
![Apple Slips to Fifth in China's Smartphone Market with 9% Decline [Report]](https://www.iclarified.com/images/news/97065/97065/97065-640.jpg)