2226. Maximum Candies Allocated to K Children

2226. Maximum Candies Allocated to K Children Difficulty: Medium Topics: Array, Binary Search You are given a 0-indexed integer array candies. Each element in the array denotes a pile of candies of size candies[i]. You can divide each pile into any number of sub piles, but you cannot merge two piles together. You are also given an integer k. You should allocate piles of candies to k children such that each child gets the same number of candies. Each child can be allocated candies from only one pile of candies and some piles of candies may go unused. Return the maximum number of candies each child can get. Example 1: Input: candies = [5,8,6], k = 3 Output: 5 Explanation: We can divide candies[1] into 2 piles of size 5 and 3, and candies[2] into 2 piles of size 5 and 1. We now have five piles of candies of sizes 5, 5, 3, 5, and 1. We can allocate the 3 piles of size 5 to 3 children. It can be proven that each child cannot receive more than 5 candies. Example 2: Input: candies = [2,5], k = 11 Output: 0 Explanation: There are 11 children but only 7 candies in total, so it is impossible to ensure each child receives at least one candy. Thus, each child gets no candy and the answer is 0. Constraints: 1 Explanation: Initial Check: First, we check if the total number of candies is less than k. If so, it's impossible to distribute even one candy to each child, so we return 0. Binary Search Setup: We initialize the binary search with left set to 1 and right set to the maximum pile size in the candies array. Mid Calculation: For each midpoint mid during the binary search, we calculate the total number of sub-piles each pile can contribute when divided into mid candies. Check Feasibility: If the total number of sub-piles is at least k, mid is a feasible solution, and we try for a higher value by adjusting the search range. If not, we adjust the range to look for a smaller value. Early Termination: During the sum calculation, if we accumulate enough sub-piles early, we break out of the loop to save computation time. This approach efficiently narrows down the possible values using binary search, ensuring we find the maximum number of candies each child can receive in logarithmic time relative to the maximum pile size, making it suitable for large input sizes. Contact Links If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks

Mar 14, 2025 - 18:29

Difficulty: Medium

Topics: Array, Binary Search

You are given a 0-indexed integer array candies. Each element in the array denotes a pile of candies of size candies[i]. You can divide each pile into any number of sub piles, but you cannot merge two piles together.

You are also given an integer k. You should allocate piles of candies to k children such that each child gets the same number of candies. Each child can be allocated candies from only one pile of candies and some piles of candies may go unused.

Return the maximum number of candies each child can get.

Example 1:

Input: candies = [5,8,6], k = 3
Output: 5
Explanation: We can divide candies[1] into 2 piles of size 5 and 3, and candies[2] into 2 piles of size 5 and 1. We now have five piles of candies of sizes 5, 5, 3, 5, and 1. We can allocate the 3 piles of size 5 to 3 children. It can be proven that each child cannot receive more than 5 candies.

Example 2:

Input: candies = [2,5], k = 11
Output: 0
Explanation: There are 11 children but only 7 candies in total, so it is impossible to ensure each child receives at least one candy. Thus, each child gets no candy and the answer is 0.

Constraints:

1 <= candies.length <= 10⁵
1 <= candies[i] <= 10⁷
1 <= k <= 10¹²

Hint:

For a fixed number of candies c, how can you check if each child can get c candies?
Use binary search to find the maximum c as the answer.

Solution:

We need to determine the maximum number of candies each child can get such that each child receives the same number of candies from a single pile (or sub-pile). The solution involves using binary search to efficiently find this maximum number of candies.

Approach

Problem Analysis: The key insight is to recognize that for a given number of candies c, we can check if it's possible to distribute c candies to each of k children by summing the number of sub-piles each pile can contribute (each sub-pile must have at least c candies). This sum must be at least k for the distribution to be possible.
Binary Search: We use binary search to efficiently find the maximum value of c. The search range is from 1 to the maximum pile size in the candies array.
Early Termination: During each iteration of the binary search, if we accumulate enough sub-piles to meet the requirement k, we can terminate early to save computation time.

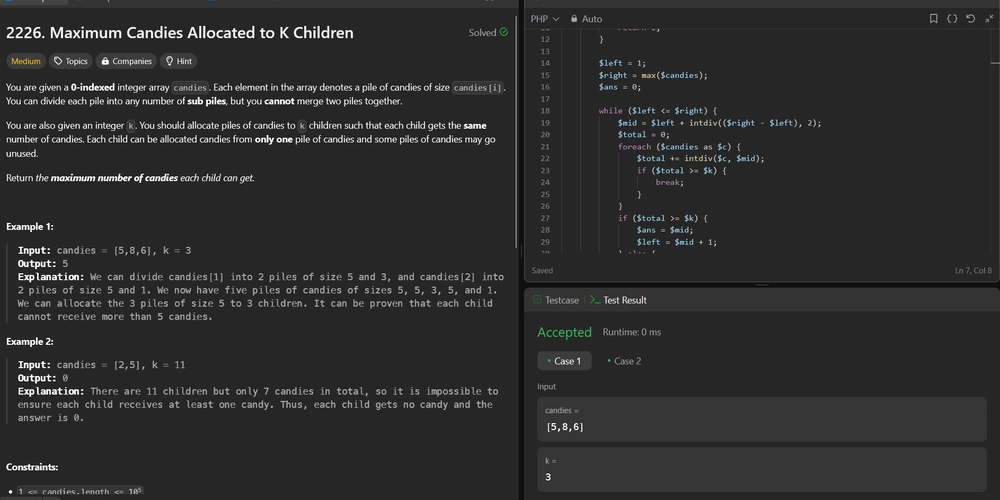
Let's implement this solution in PHP: 2226. Maximum Candies Allocated to K Children


/**
 * @param Integer[] $candies
 * @param Integer $k
 * @return Integer
 */
function maximumCandies($candies, $k) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example Test Cases
echo maximumCandies([5,8,6], 3) . "\n"; // Output: 5
echo maximumCandies([2,5], 11) . "\n"; // Output: 0
?>

Explanation:

Initial Check: First, we check if the total number of candies is less than k. If so, it's impossible to distribute even one candy to each child, so we return 0.
Binary Search Setup: We initialize the binary search with left set to 1 and right set to the maximum pile size in the candies array.
Mid Calculation: For each midpoint mid during the binary search, we calculate the total number of sub-piles each pile can contribute when divided into mid candies.
Check Feasibility: If the total number of sub-piles is at least k, mid is a feasible solution, and we try for a higher value by adjusting the search range. If not, we adjust the range to look for a smaller value.
Early Termination: During the sum calculation, if we accumulate enough sub-piles early, we break out of the loop to save computation time.

This approach efficiently narrows down the possible values using binary search, ensuring we find the maximum number of candies each child can receive in logarithmic time relative to the maximum pile size, making it suitable for large input sizes.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks