บทความ "K-Means Clustering: Clustering Unsupervised Machine Learning"

อธิบายแนวคิดและการใช้งานของอัลกอริทึม K-Means Clustering ซึ่งเป็นเทคนิคการเรียนรู้ของเครื่องแบบไม่มีผู้สอน (Unsupervised Learning) ที่ใช้ในการแบ่งกลุ่มข้อมูลที่ไม่มีป้ายกำกับล่วงหน้า K-Means Clustering คืออะไร? K-Means Clustering เป็นอัลกอริทึมที่ใช้ในการแบ่งกลุ่มข้อมูล (Clustering) โดยไม่ต้องมีป้ายกำกับ (Label) ล่วงหน้า เป้าหมายคือการจัดกลุ่มข้อมูลที่มีลักษณะคล้ายกันเข้าด้วยกัน โดยกำหนดจำนวนกลุ่มล่วงหน้าเป็นค่า K แต่ละกลุ่มจะมีจุดศูนย์กลาง (Centroid) ซึ่งเป็นค่าเฉลี่ยของข้อมูลในกลุ่มนั้น ขั้นตอนการทำงานของ K-Means Clustering 1.กำหนดค่า K: เลือกจำนวนกลุ่มที่ต้องการแบ่งข้อมูล สุ่มจุดศูนย์กลางเริ่มต้น: สุ่มเลือก K จุดจากข้อมูลเป็นจุดศูนย์กลางเริ่มต้น จัดกลุ่มข้อมูล: คำนวณระยะห่างระหว่างแต่ละจุดข้อมูลกับจุดศูนย์กลาง แล้วจัดกลุ่มข้อมูลให้ใกล้กับจุดศูนย์กลางที่สุด อัปเดตจุดศูนย์กลาง: คำนวณค่าเฉลี่ยของข้อมูลในแต่ละกลุ่มใหม่ เพื่อหาจุดศูนย์กลางใหม่ ทำซ้ำขั้นตอนที่ 3 และ 4: ทำซ้ำจนกว่าจุดศูนย์กลางจะไม่เปลี่ยนแปลงมากนัก หรือถึงจำนวนรอบที่กำหนด แนวคิดสำคัญใน K-Means Clustering จุดศูนย์กลาง (Centroid): ตำแหน่งเฉลี่ยของข้อมูลในแต่ละกลุ่ม Inertia: ค่าผลรวมของระยะห่างระหว่างจุดข้อมูลกับจุดศูนย์กลางของกลุ่ม ใช้ในการวัดความกระชับของกลุ่ม การเลือกค่า K: สามารถใช้วิธี Elbow Method หรือ Silhouette Analysis เพื่อช่วยในการตัดสินใจเลือกจำนวนกลุ่มที่เหมาะสม การใช้งาน K-Means Clustering ด้วย Python ในบทความมีตัวอย่างการใช้งาน K-Means Clustering ด้วยภาษา Python โดยใช้ไลบรารี scikit-learn ตัวอย่างโค้ด Python 1. นำเข้าไลบรารี import numpy as np import matplotlib.pyplot as plt from sklearn.cluster import KMeans บล็อกนี้จะนำเข้าไลบรารีที่จำเป็นสำหรับการจัดการและการวางแผนข้อมูล 2. สร้างข้อมูลตัวอย่างที่มี 3 คลัสเตอร์ np.random.seed(42) # For reproducibility n_samples = 300 # Cluster 1: Centered at (0, 0) X1 = np.random.randn(n_samples // 3, 2) * 0.5 # Cluster 2: Centered at (3, 3) X2 = np.random.randn(n_samples // 3, 2) * 0.5 + [3, 3] # Cluster 3: Centered at (-2, 3) X3 = np.random.randn(n_samples // 3, 2) * 0.5 + [-2, 3] # Combine all clusters X = np.vstack((X1, X2, X3)) บล็อกนี้สร้างข้อมูลสังเคราะห์สำหรับคลัสเตอร์สามคลัสเตอร์ที่ตั้งอยู่ในพื้นที่ฟีเจอร์ต่างๆ 3. ดำเนินการจัดกลุ่ม k-Means n_clusters = 3 kmeans = KMeans(n_clusters=n_clusters, random_state=42, n_init=10) cluster_labels = kmeans.fit_predict(X) บล็อกนี้จะเริ่มต้นอัลกอริทึม k-Means ด้วยจำนวนคลัสเตอร์ที่ระบุ และปรับให้เข้ากับชุดข้อมูล โดยทำนายป้ายคลัสเตอร์สำหรับจุดข้อมูลแต่ละจุด 4. แสดงภาพผลลัพธ์การจัดกลุ่ม plt.figure(figsize=(12, 8)) # Plot the data points scatter = plt.scatter(X[:, 0], X[:, 1], c=cluster_labels, cmap='viridis', alpha=0.7) # Plot the cluster centers centers = kmeans.cluster_centers_ plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x', s=200, linewidths=3) plt.title(f'K-means Clustering (k={n_clusters})') plt.xlabel('Feature 1') plt.ylabel('Feature 2') plt.colorbar(scatter) # Add text annotations for each cluster for i, center in enumerate(centers): plt.annotate(f'Cluster {i}', center, fontsize=12, fontweight='bold', xytext=(5, 5), textcoords='offset points') plt.show() บล็อกนี้แสดงภาพผลลัพธ์การจัดกลุ่ม โดยแสดงจุดข้อมูลที่มีสีตามป้ายกำกับกลุ่ม และทำเครื่องหมายจุดศูนย์กลางกลุ่มด้วยสัญลักษณ์ 'X' สีแดง ผลลัพท์ เรามาลองทำเป็นชุดข้อมูลแบบ วงกลมกัน ขั้นตอนที่ 1 เป็นคำสั่งสำหรับ นำเข้า (import) ฟังก์ชัน make_circles จากไลบรารี scikit-learn make_circles จะใช้สำหรับสร้าง ข้อมูลจำลองที่อยู่เป็นรูปวงกลมซ้อนกัน 2 วง from sklearn.datasets import make_circles ขั้นตอนที่ 2 สร้างข้อมูลวงกลมซ้อนกัน X, y = make_circles(n_samples=300, factor=0.5, noise=0.05) อธิบายพารามิเตอร์: n_samples=300 → สร้างข้อมูลทั้งหมด 300 จุด factor=0.5 → กำหนด สัดส่วนของวงในกับวงนอก (วงใน = ครึ่งหนึ่งของวงนอก) noise=0.05 → เพิ่มความสุ่มให้กับตำแหน่งจุดเล็กน้อย ทำให้ดูเป็นธรรมชาติ ไม่เรียงสวยเป๊ะ ผลลัพธ์: X → เป็น ข้อมูลตำแหน่งจุด (x, y) ขนาด (300, 2) คือ 300 แถว 2 คอลัมน์ y → เป็น ป้าย label จริงของจุด (0 หรือ 1) บอกว่าวงไหน (ใช้เพื่อเปรียบเทียบ ไม่ได้ใช้ใน KMeans) ขั้นตอนที่ 3 ใช้อัลกอริทึม K-Means เพื่อจัดกลุ่มข้อมูล kmeans = KMeans(n_clusters=2) สร้างโมเดล KMeans จาก sklearn.cluster กำหนดให้จัดกลุ่มเป็น 2 กลุ่ม (n_clusters=2) เพราะเรารู้ว่ามี 2 วง kmeans.fit(X) ฝึกโมเดล (Train) โดยใช้ข้อมูล X KMeans จะพยายามจัดกลุ่มข้อมูลให้ดีที่สุดโดยอิงจากระยะห่างของจุดกับ "จุดศูนย์กลางกลุ่ม" (centroid) y_kmeans = kmeans.predict(X) หลังฝึกเสร็จ เราให้โมเดล ทำนายว่าจุดแต่ละจุดควรอยู่ในกลุ่มไหน (คลัสเตอร์ที่ 0 หรือ 1) ผลลัพธ์ y_kmeans เป็น array ที่บอกว่าแต่ละจุดอยู่กลุ่มไหน (เช่น [1, 0, 1, 0, ...]) ขั้นตอนที่ 4แสดงผลการจัดกลุ่มด้วยกราฟ plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis') ใช้ matplotlib.pyplot ในการสร้าง scatter plot X[:, 0] → พิกัดแกน X (ค่าคอลัมน์ที่ 0) X[:, 1] → พิกัดแกน Y (ค่าคอลัมน์ที่ 1) c=y_kmeans → ระบายสีแต่ละจุดตามกลุ่มที่ KMeans จัดไว้ s=50 → กำหนดขนาดจุด cmap='viridis' → กำหนดชุดสีที่ใช้ centers = kmeans.cluster_centers_ ดึงตำแหน่งของ ศูนย์กลางกลุ่ม (centroid) ที่ KMeans คำนวณได้ เป

Apr 16, 2025 - 20:34

บทความ "K-Means Clustering: Clustering Unsupervised Machine Learning"

อธิบายแนวคิดและการใช้งานของอัลกอริทึม K-Means Clustering ซึ่งเป็นเทคนิคการเรียนรู้ของเครื่องแบบไม่มีผู้สอน (Unsupervised Learning) ที่ใช้ในการแบ่งกลุ่มข้อมูลที่ไม่มีป้ายกำกับล่วงหน้า
K-Means Clustering คืออะไร?
K-Means Clustering เป็นอัลกอริทึมที่ใช้ในการแบ่งกลุ่มข้อมูล (Clustering) โดยไม่ต้องมีป้ายกำกับ (Label) ล่วงหน้า เป้าหมายคือการจัดกลุ่มข้อมูลที่มีลักษณะคล้ายกันเข้าด้วยกัน โดยกำหนดจำนวนกลุ่มล่วงหน้าเป็นค่า K แต่ละกลุ่มจะมีจุดศูนย์กลาง (Centroid) ซึ่งเป็นค่าเฉลี่ยของข้อมูลในกลุ่มนั้น

ขั้นตอนการทำงานของ K-Means Clustering

1.กำหนดค่า K: เลือกจำนวนกลุ่มที่ต้องการแบ่งข้อมูล

สุ่มจุดศูนย์กลางเริ่มต้น: สุ่มเลือก K จุดจากข้อมูลเป็นจุดศูนย์กลางเริ่มต้น
จัดกลุ่มข้อมูล: คำนวณระยะห่างระหว่างแต่ละจุดข้อมูลกับจุดศูนย์กลาง แล้วจัดกลุ่มข้อมูลให้ใกล้กับจุดศูนย์กลางที่สุด
อัปเดตจุดศูนย์กลาง: คำนวณค่าเฉลี่ยของข้อมูลในแต่ละกลุ่มใหม่ เพื่อหาจุดศูนย์กลางใหม่
ทำซ้ำขั้นตอนที่ 3 และ 4: ทำซ้ำจนกว่าจุดศูนย์กลางจะไม่เปลี่ยนแปลงมากนัก หรือถึงจำนวนรอบที่กำหนด

แนวคิดสำคัญใน K-Means Clustering
จุดศูนย์กลาง (Centroid): ตำแหน่งเฉลี่ยของข้อมูลในแต่ละกลุ่ม

Inertia: ค่าผลรวมของระยะห่างระหว่างจุดข้อมูลกับจุดศูนย์กลางของกลุ่ม ใช้ในการวัดความกระชับของกลุ่ม

การเลือกค่า K: สามารถใช้วิธี Elbow Method หรือ Silhouette Analysis เพื่อช่วยในการตัดสินใจเลือกจำนวนกลุ่มที่เหมาะสม

การใช้งาน K-Means Clustering ด้วย Python
ในบทความมีตัวอย่างการใช้งาน K-Means Clustering ด้วยภาษา Python โดยใช้ไลบรารี scikit-learn

ตัวอย่างโค้ด Python 1. นำเข้าไลบรารี

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

บล็อกนี้จะนำเข้าไลบรารีที่จำเป็นสำหรับการจัดการและการวางแผนข้อมูล

2. สร้างข้อมูลตัวอย่างที่มี 3 คลัสเตอร์

np.random.seed(42)  # For reproducibility
n_samples = 300

# Cluster 1: Centered at (0, 0)
X1 = np.random.randn(n_samples // 3, 2) * 0.5

# Cluster 2: Centered at (3, 3)
X2 = np.random.randn(n_samples // 3, 2) * 0.5 + [3, 3]

# Cluster 3: Centered at (-2, 3)
X3 = np.random.randn(n_samples // 3, 2) * 0.5 + [-2, 3]

# Combine all clusters
X = np.vstack((X1, X2, X3))

บล็อกนี้สร้างข้อมูลสังเคราะห์สำหรับคลัสเตอร์สามคลัสเตอร์ที่ตั้งอยู่ในพื้นที่ฟีเจอร์ต่างๆ

3. ดำเนินการจัดกลุ่ม k-Means

n_clusters = 3
kmeans = KMeans(n_clusters=n_clusters, random_state=42, n_init=10)
cluster_labels = kmeans.fit_predict(X)

บล็อกนี้จะเริ่มต้นอัลกอริทึม k-Means ด้วยจำนวนคลัสเตอร์ที่ระบุ และปรับให้เข้ากับชุดข้อมูล โดยทำนายป้ายคลัสเตอร์สำหรับจุดข้อมูลแต่ละจุด

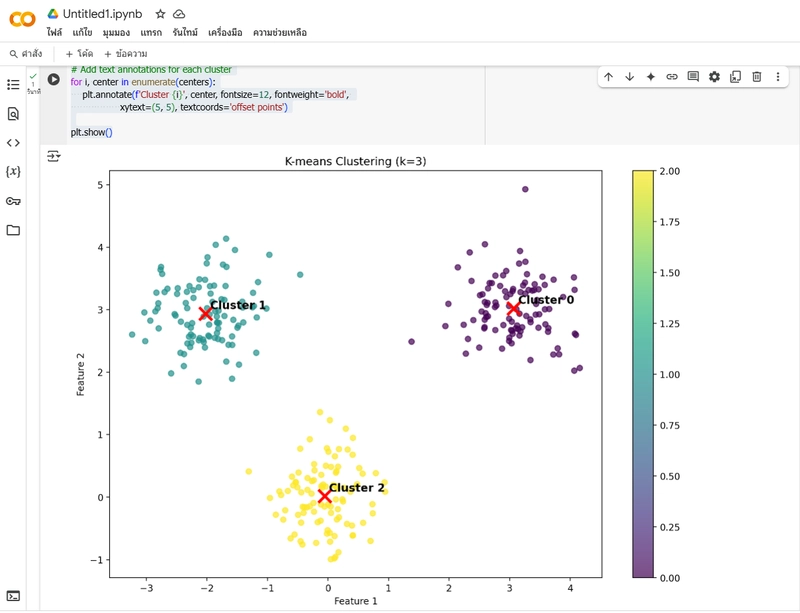
4. แสดงภาพผลลัพธ์การจัดกลุ่ม

plt.figure(figsize=(12, 8))

# Plot the data points
scatter = plt.scatter(X[:, 0], X[:, 1], c=cluster_labels, cmap='viridis', alpha=0.7)

# Plot the cluster centers
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x', s=200, linewidths=3)

plt.title(f'K-means Clustering (k={n_clusters})')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.colorbar(scatter)

# Add text annotations for each cluster
for i, center in enumerate(centers):
    plt.annotate(f'Cluster {i}', center, fontsize=12, fontweight='bold', 
                 xytext=(5, 5), textcoords='offset points')

plt.show()

บล็อกนี้แสดงภาพผลลัพธ์การจัดกลุ่ม โดยแสดงจุดข้อมูลที่มีสีตามป้ายกำกับกลุ่ม และทำเครื่องหมายจุดศูนย์กลางกลุ่มด้วยสัญลักษณ์ 'X' สีแดง

ผลลัพท์

เรามาลองทำเป็นชุดข้อมูลแบบ วงกลมกัน
ขั้นตอนที่ 1 เป็นคำสั่งสำหรับ นำเข้า (import)
ฟังก์ชัน make_circles จากไลบรารี scikit-learn make_circles จะใช้สำหรับสร้าง ข้อมูลจำลองที่อยู่เป็นรูปวงกลมซ้อนกัน 2 วง

from sklearn.datasets import make_circles

ขั้นตอนที่ 2 สร้างข้อมูลวงกลมซ้อนกัน

X, y = make_circles(n_samples=300, factor=0.5, noise=0.05)

อธิบายพารามิเตอร์:
n_samples=300 → สร้างข้อมูลทั้งหมด 300 จุด

factor=0.5 → กำหนด สัดส่วนของวงในกับวงนอก (วงใน = ครึ่งหนึ่งของวงนอก)

noise=0.05 → เพิ่มความสุ่มให้กับตำแหน่งจุดเล็กน้อย ทำให้ดูเป็นธรรมชาติ ไม่เรียงสวยเป๊ะ

ผลลัพธ์:
X → เป็น ข้อมูลตำแหน่งจุด (x, y) ขนาด (300, 2) คือ 300 แถว 2 คอลัมน์

y → เป็น ป้าย label จริงของจุด (0 หรือ 1) บอกว่าวงไหน (ใช้เพื่อเปรียบเทียบ ไม่ได้ใช้ใน KMeans)

ขั้นตอนที่ 3 ใช้อัลกอริทึม K-Means เพื่อจัดกลุ่มข้อมูล

kmeans = KMeans(n_clusters=2)

สร้างโมเดล KMeans จาก sklearn.cluster

กำหนดให้จัดกลุ่มเป็น 2 กลุ่ม (n_clusters=2) เพราะเรารู้ว่ามี 2 วง

kmeans.fit(X)

ฝึกโมเดล (Train) โดยใช้ข้อมูล X

KMeans จะพยายามจัดกลุ่มข้อมูลให้ดีที่สุดโดยอิงจากระยะห่างของจุดกับ "จุดศูนย์กลางกลุ่ม" (centroid)

y_kmeans = kmeans.predict(X)

หลังฝึกเสร็จ เราให้โมเดล ทำนายว่าจุดแต่ละจุดควรอยู่ในกลุ่มไหน (คลัสเตอร์ที่ 0 หรือ 1)

ผลลัพธ์ y_kmeans เป็น array ที่บอกว่าแต่ละจุดอยู่กลุ่มไหน (เช่น [1, 0, 1, 0, ...])

ขั้นตอนที่ 4แสดงผลการจัดกลุ่มด้วยกราฟ

plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')

ใช้ matplotlib.pyplot ในการสร้าง scatter plot

X[:, 0] → พิกัดแกน X (ค่าคอลัมน์ที่ 0)

X[:, 1] → พิกัดแกน Y (ค่าคอลัมน์ที่ 1)

c=y_kmeans → ระบายสีแต่ละจุดตามกลุ่มที่ KMeans จัดไว้

s=50 → กำหนดขนาดจุด

cmap='viridis' → กำหนดชุดสีที่ใช้

centers = kmeans.cluster_centers_

ดึงตำแหน่งของ ศูนย์กลางกลุ่ม (centroid) ที่ KMeans คำนวณได้

เป็น array ขนาด (2, 2) → เพราะมี 2 กลุ่ม และแต่ละ centroid มี 2 ค่าพิกัด (x, y)

plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5)

วาด จุดศูนย์กลางกลุ่ม เป็นสีดำ

s=200 → ขนาดจุดใหญ่ชัดเจน

alpha=0.5 → กำหนดความโปร่งใสให้มองเห็นพื้นหลังได้เล็กน้อย

plt.title("K-Means on Circular Data")

ตั้งชื่อกราฟให้ดูสวยงามและสื่อความหมาย

ขั้นตอนสุดท้าย สั่งให้แสดงผลกราฟทั้งหมดที่วาดไว้

plt.show()

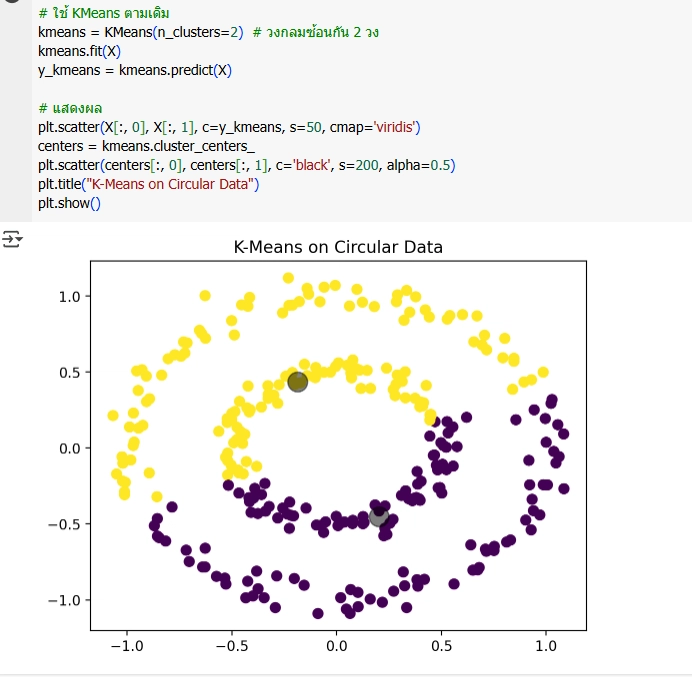
ผลลัพท์

สรุปสั้น
สร้างข้อมูลวงกลมซ้อนกัน

ใช้ KMeans แบ่งข้อมูลเป็น 2 กลุ่ม

วาดกราฟแสดงการจัดกลุ่ม พร้อมจุดศูนย์กลางของแต่ละกลุ่ม**

สรุป
การแสดงภาพผลลัพธ์ของการจัดกลุ่มด้วย K-Means ช่วยให้เราเห็นได้ชัดเจนว่าข้อมูลถูกแบ่งออกเป็นแต่ละคลัสเตอร์อย่างไร ซึ่งช่วยให้เข้าใจโครงสร้างของข้อมูลและรูปแบบการกระจายตัวของแต่ละกลุ่มได้ง่ายขึ้น

หากคุณทำตามขั้นตอนที่มีโครงสร้างชัดเจน เช่น การเลือกจำนวนคลัสเตอร์ที่เหมาะสม การใช้เครื่องมือสำหรับแสดงภาพ และการวิเคราะห์ผลลัพธ์ คุณก็จะสามารถนำ K-Means ไปใช้กับชุดข้อมูลต่างๆ ได้อย่างมีประสิทธิภาพ และยังได้ข้อมูลเชิงลึกที่เป็นประโยชน์เกี่ยวกับลักษณะพื้นฐานของข้อมูลเหล่านั้นอีกด้วย