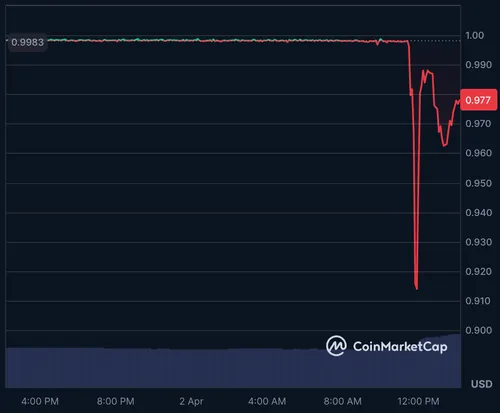
Solves a standard 9x9 Sudoku puzzle ensuring that each row, column, and 3x3 subgrid contains numbers 1-9.
# Sudoku Solver - Backtracking # Description: Solves a standard 9x9 Sudoku puzzle ensuring that each row, column, and 3x3 subgrid contains numbers 1-9. def is_valid_placement(board, row, col, num): """ Check if it's valid to place a number in a specific cell. Args: board (list of list of int): 9x9 Sudoku grid row (int): Row index of the cell col (int): Column index of the cell num (int): Number to place in the cell Returns: bool: True if placement is valid, False otherwise """ # Check row for x in range(9): if board[row][x] == num: return False # Check column for x in range(9): if board[x][col] == num: return False # Check 3x3 sub-grid start_row = row - row % 3 start_col = col - col % 3 for i in range(3): for j in range(3): if board[start_row + i][start_col + j] == num: return False return True def find_empty_cell(board): """ Find an empty cell in the Sudoku board. Args: board (list of list of int): 9x9 Sudoku grid Returns: tuple or None: (row, col) of the first empty cell, or None if no empty cell exists """ for row in range(9): for col in range(9): if board[row][col] == 0: return row, col return None def solve_sudoku(board): """ Solve a Sudoku puzzle using backtracking algorithm. This solver modifies the board in-place. It tries to fill empty cells with numbers 1-9 while maintaining Sudoku rules. Time Complexity: O(9^(n*n)), where n is board size (9 in standard Sudoku) Space Complexity: O(n*n) due to recursion stack Args: board (list of list of int): 9x9 Sudoku grid (0 represents empty cells) Returns: bool: True if a solution is found, False otherwise Example: board = [ [5, 3, 0, 0, 7, 0, 0, 0, 0], [6, 0, 0, 1, 9, 5, 0, 0, 0], [0, 9, 8, 0, 0, 0, 0, 6, 0], [8, 0, 0, 0, 6, 0, 0, 0, 3], [4, 0, 0, 8, 0, 3, 0, 0, 1], [7, 0, 0, 0, 2, 0, 0, 0, 6], [0, 6, 0, 0, 0, 0, 2, 8, 0], [0, 0, 0, 4, 1, 9, 0, 0, 5], [0, 0, 0, 0, 8, 0, 0, 7, 9] ] solve_sudoku(board) # Solves the board in-place """ # Find an empty cell empty_cell = find_empty_cell(board) # If no empty cell, puzzle is solved if not empty_cell: return True row, col = empty_cell # Try placing numbers 1-9 for num in range(1, 10): # Check if number can be placed if is_valid_placement(board, row, col, num): # Place the number board[row][col] = num # Recursively try to solve the rest of the board if solve_sudoku(board): return True # If placement doesn't lead to solution, backtrack board[row][col] = 0 # No solution found return False def print_sudoku(board): """ Print the Sudoku board in a readable format. Args: board (list of list of int): 9x9 Sudoku grid """ for i, row in enumerate(board): # Print horizontal separators for 3x3 sub-grids if i % 3 == 0 and i != 0: print("-" * 21) for j, num in enumerate(row): # Print vertical separators for 3x3 sub-grids if j % 3 == 0 and j != 0: print("|", end=" ") print(num, end=" ") print() # New line after each row

# Sudoku Solver - Backtracking
# Description: Solves a standard 9x9 Sudoku puzzle ensuring that each row, column, and 3x3 subgrid contains numbers 1-9.
def is_valid_placement(board, row, col, num):
"""
Check if it's valid to place a number in a specific cell.
Args:
board (list of list of int): 9x9 Sudoku grid
row (int): Row index of the cell
col (int): Column index of the cell
num (int): Number to place in the cell
Returns:
bool: True if placement is valid, False otherwise
"""
# Check row
for x in range(9):
if board[row][x] == num:
return False
# Check column
for x in range(9):
if board[x][col] == num:
return False
# Check 3x3 sub-grid
start_row = row - row % 3
start_col = col - col % 3
for i in range(3):
for j in range(3):
if board[start_row + i][start_col + j] == num:
return False
return True
def find_empty_cell(board):
"""
Find an empty cell in the Sudoku board.
Args:
board (list of list of int): 9x9 Sudoku grid
Returns:
tuple or None: (row, col) of the first empty cell, or None if no empty cell exists
"""
for row in range(9):
for col in range(9):
if board[row][col] == 0:
return row, col
return None
def solve_sudoku(board):
"""
Solve a Sudoku puzzle using backtracking algorithm.
This solver modifies the board in-place. It tries to fill empty cells
with numbers 1-9 while maintaining Sudoku rules.
Time Complexity: O(9^(n*n)), where n is board size (9 in standard Sudoku)
Space Complexity: O(n*n) due to recursion stack
Args:
board (list of list of int): 9x9 Sudoku grid
(0 represents empty cells)
Returns:
bool: True if a solution is found, False otherwise
Example:
board = [
[5, 3, 0, 0, 7, 0, 0, 0, 0],
[6, 0, 0, 1, 9, 5, 0, 0, 0],
[0, 9, 8, 0, 0, 0, 0, 6, 0],
[8, 0, 0, 0, 6, 0, 0, 0, 3],
[4, 0, 0, 8, 0, 3, 0, 0, 1],
[7, 0, 0, 0, 2, 0, 0, 0, 6],
[0, 6, 0, 0, 0, 0, 2, 8, 0],
[0, 0, 0, 4, 1, 9, 0, 0, 5],
[0, 0, 0, 0, 8, 0, 0, 7, 9]
]
solve_sudoku(board) # Solves the board in-place
"""
# Find an empty cell
empty_cell = find_empty_cell(board)
# If no empty cell, puzzle is solved
if not empty_cell:
return True
row, col = empty_cell
# Try placing numbers 1-9
for num in range(1, 10):
# Check if number can be placed
if is_valid_placement(board, row, col, num):
# Place the number
board[row][col] = num
# Recursively try to solve the rest of the board
if solve_sudoku(board):
return True
# If placement doesn't lead to solution, backtrack
board[row][col] = 0
# No solution found
return False
def print_sudoku(board):
"""
Print the Sudoku board in a readable format.
Args:
board (list of list of int): 9x9 Sudoku grid
"""
for i, row in enumerate(board):
# Print horizontal separators for 3x3 sub-grids
if i % 3 == 0 and i != 0:
print("-" * 21)
for j, num in enumerate(row):
# Print vertical separators for 3x3 sub-grids
if j % 3 == 0 and j != 0:
print("|", end=" ")
print(num, end=" ")
print() # New line after each row






































































































































































![[The AI Show Episode 142]: ChatGPT’s New Image Generator, Studio Ghibli Craze and Backlash, Gemini 2.5, OpenAI Academy, 4o Updates, Vibe Marketing & xAI Acquires X](https://www.marketingaiinstitute.com/hubfs/ep%20142%20cover.png)

























































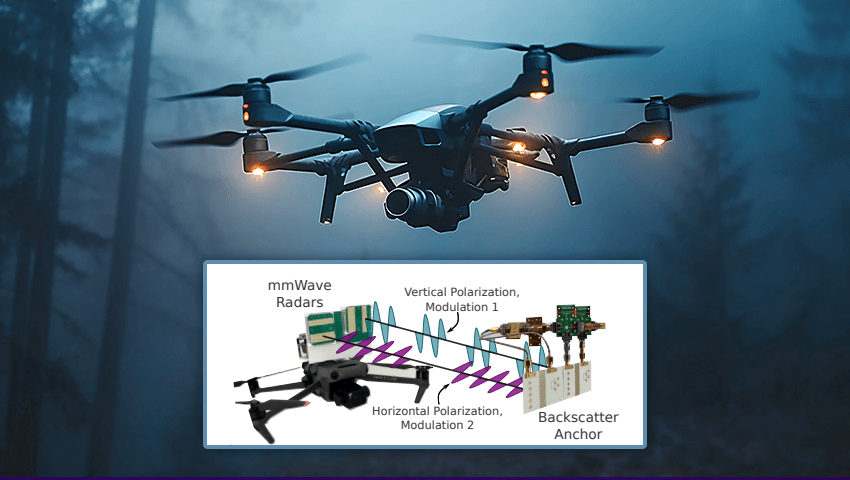











































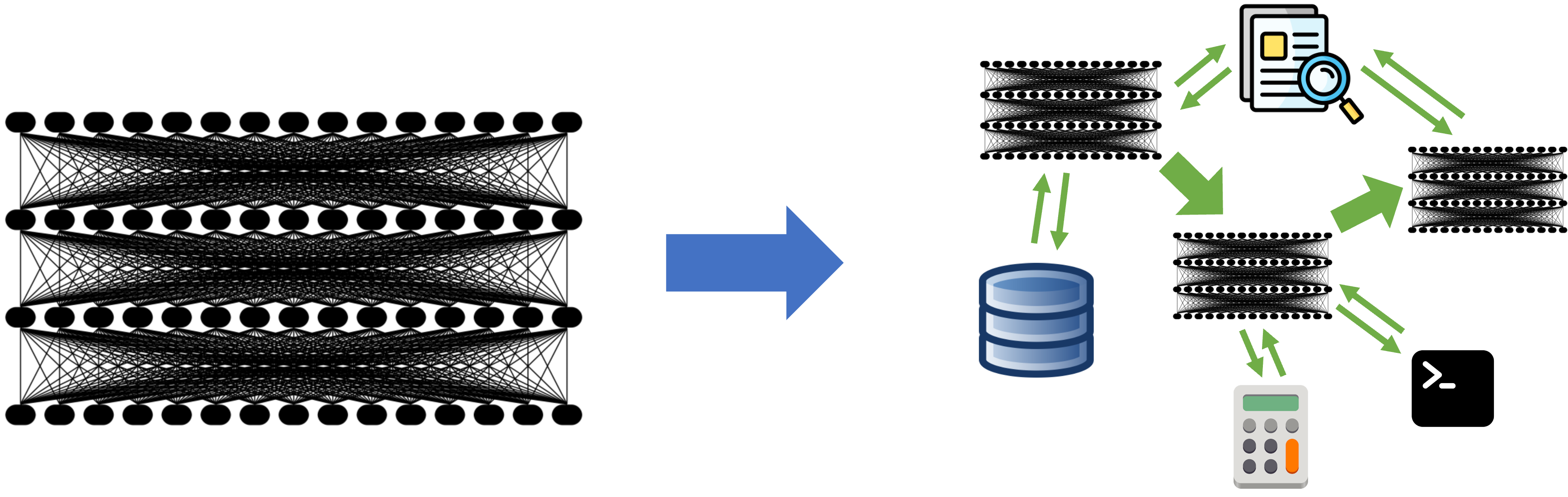












![[DEALS] The Premium Learn to Code Certification Bundle (97% off) & Other Deals Up To 98% Off – Offers End Soon!](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)


![From drop-out to software architect with Jason Lengstorf [Podcast #167]](https://cdn.hashnode.com/res/hashnode/image/upload/v1743796461357/f3d19cd7-e6f5-4d7c-8bfc-eb974bc8da68.png?#)



































































































.png?#)






























_Christophe_Coat_Alamy.jpg?#)
 (1).webp?#)


































































































![Apple Considers Delaying Smart Home Hub Until 2026 [Gurman]](https://www.iclarified.com/images/news/96946/96946/96946-640.jpg)
![iPhone 17 Pro Won't Feature Two-Toned Back [Gurman]](https://www.iclarified.com/images/news/96944/96944/96944-640.jpg)
![Tariffs Threaten Apple's $999 iPhone Price Point in the U.S. [Gurman]](https://www.iclarified.com/images/news/96943/96943/96943-640.jpg)