¿Cuál es el valor de PI?

Pero... ¿por qué? Curiosidad: el 14 de marzo fue el día de PI! Por aquello de 3.14 -> Marzo, 14 (los ingleses ponen delante el número del mes). ¿Pero... qué es PI? El número PI es la relación entre el perímetro pr y el diámetro d (es decir, el doble del radio r, que es 2r), de un círculo. Más abajo se toma la definición del perímetro de la circunferencia, y se reordenan los términos para finalmente despejar PI en lugar de pr. pr = 2 PI r pr = 2r PI PI = pr / 2r El problema de estas ecuaciones es que son muy poco prácticas. Es decir, ¿puedo medir el perímetro de un círculo con una cuerda, dividirlo por el radio, y obtener PI? Difícilmente. PI en realidad es "un poco más" que tres, y es muy difícil afinar lo suficiente como para poder medir ese "poco más" de forma que tenga sentido. Para empezar, tendría que ser una cuerda muy, muy larga, de forma que podamos "afinar" o aproximar lo suficiente. Después, habría que encontrar el círculo adecuado. ¿Una tubería gruesa? Lo ideal sería que el radio fuera 0,5 (¿metros, kilómetros?) para que el diámetro fuese 1, y por lo tanto PI fuese simplemente el perímetro. No es imposible, pero es muy, muy difícil. Hace algún tiempo, estaba curioseando por Youtube, cuando me encontré con un vídeo en el que el presentador decía que PI no era 3.14, sino 3.12, sino recuerdo mal. Como prueba de que este valor alternativo era el correcto, afirmaba que "a la NASA se le caían los satélites" (¿?), hasta que cambiaron el valor de PI. Además, proporcionaba un software escrito en C#. Este programa había sido eliminado de la web, y a pesar de haberle escrito para pedírselo, no obtuve ninguna respuesta. ¿Por qué le di tanta importancia a aquel vídeo? Porque me interesaba calcular el valor de PI de alguna forma "no matemática", sencilla de entender (yo no soy matemático). Y aquel vídeo me dio una idea: representar la circunferencia en un canvas cualquiera, y contar los puntos para saber cuál era su perímetro. Así, mi hipótesis era que cuanto mayor fuera su radio, la imprecisión de utilizar puntos en una pantalla se diluiría, y se aproximaría poco a poco, convergiendo hacia el valor de PI. Arriba se pueden ver dos círculos en una malla de 8x8 puntos. Incluso se puede apreciar en un ejemplo tan limitado que, cuanto más se aumenta el radio, más se "parece" a un círculo real. Hardware y software El navegador empleado fue Falkon v24.12.3, en una máquina Intel Core i7-7700 con 32GB de RAM corriendo Manjaro Linux sobre un Kernel 6.13.7. Calculando el valor de PI mediante el perímetro Dicho y hecho, preparé usando HTML5 un código JavaScript que calcularía el valor de PI. Exploraremos primero la parte superior, que se basa en el perímetro de un círculo. Empezamos con un valor de radio r = 3. Parece un inicio prometedor... ¿no? La idea es que poco a poco, a medida que aumentemos el radio, vayamos obteniendo un valor que se vaya afianzando. Por ejemplo, partir de 3 y pasar por 3.2, y después por 3.15, y después... no sería necesariamente esta la secuencia exacta, pero bueno, se entiende la idea. El programa dibuja un círculo en la parte inferior, y cuenta los puntos para el perímetro, de forma que después pueda dividirlos por el diámetro. Cambiamos el radio en la parte superior, y pulsamos Calcular PI en la parte inferior. Un cuarto de círculo se dibujará, el programa contará los puntos, y mostrará el resultado. En cuanto al resultado, a la izquierda aparece el valor de PI calculado de forma teórica (por llamarlo de alguna forma, y poder diferenciarlos), y a la derecha aparece calculado de forma práctica, es decir, contando los puntos como ya hemos explicado. Obtuve la siguiente tabla. Radio Valor de PI 20 3 25 2.88 30 2.93 35 2.85 Mi gozo en un pozo. No estaba funcionando. El valor bajaba, y después subía. Seguí intentándolo con valores mucho más grandes, a ver si era cuestión de precisión. Radio Valor de PI 235 2.84 470 2.83 1470 2.83 6470 2.82 Quizás lo que se podía concluir era que el supuesto valor de PI iba descendiendo, centrándose en cifras claramente erróneas. Este método no funcionaba. Calculando el valor de PI mediante el área La ecuación para el perímetro de la circunferencia no es la única que involucra a PI: la del área a del círculo con radio r también lo hace: a = PI r2. Si desarrollamos este resultado para poder encontrar el valor de PI, obtenemos que: a = PI r2 PI = a / r2 Volvemos al método de dibujar el círculo y contar sus puntos; solo que esta vez, en lugar de contar los puntos de la circunferencia del círculo, contamos los puntos del interior del círculo. Dado que estamos pintando el círculo en negro sobre blanco, solo es necesario contar los puntos de color negro. Ahora desplegamos los campos dedicados al cálculo del Área pulsando en su botón [+], y descartamos la vista del perímetro pulsando en su botón [-]. Para un radio r = 20, el valor calculado de PI es 3.04. Tambi

Mar 26, 2025 - 23:44

Pero... ¿por qué?

Curiosidad: el 14 de marzo fue el día de PI! Por aquello de 3.14 -> Marzo, 14 (los ingleses ponen delante el número del mes).

¿Pero... qué es PI? El número PI es la relación entre el perímetro pr y el diámetro d (es decir, el doble del radio r, que es 2r), de un círculo. Más abajo se toma la definición del perímetro de la circunferencia, y se reordenan los términos para finalmente despejar PI en lugar de pr.

pr = 2 PI r
pr = 2r PI
PI = pr / 2r

El problema de estas ecuaciones es que son muy poco prácticas. Es decir, ¿puedo medir el perímetro de un círculo con una cuerda, dividirlo por el radio, y obtener PI? Difícilmente. PI en realidad es "un poco más" que tres, y es muy difícil afinar lo suficiente como para poder medir ese "poco más" de forma que tenga sentido. Para empezar, tendría que ser una cuerda muy, muy larga, de forma que podamos "afinar" o aproximar lo suficiente. Después, habría que encontrar el círculo adecuado. ¿Una tubería gruesa? Lo ideal sería que el radio fuera 0,5 (¿metros, kilómetros?) para que el diámetro fuese 1, y por lo tanto PI fuese simplemente el perímetro. No es imposible, pero es muy, muy difícil.

Hace algún tiempo, estaba curioseando por Youtube, cuando me encontré con un vídeo en el que el presentador decía que PI no era 3.14, sino 3.12, sino recuerdo mal. Como prueba de que este valor alternativo era el correcto, afirmaba que "a la NASA se le caían los satélites" (¿?), hasta que cambiaron el valor de PI. Además, proporcionaba un software escrito en C#. Este programa había sido eliminado de la web, y a pesar de haberle escrito para pedírselo, no obtuve ninguna respuesta.

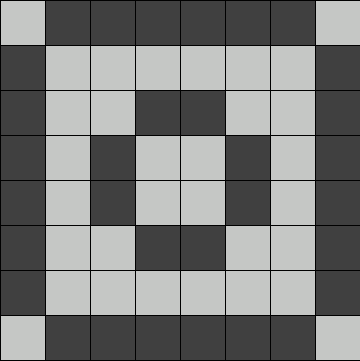
¿Por qué le di tanta importancia a aquel vídeo? Porque me interesaba calcular el valor de PI de alguna forma "no matemática", sencilla de entender (yo no soy matemático). Y aquel vídeo me dio una idea: representar la circunferencia en un canvas cualquiera, y contar los puntos para saber cuál era su perímetro. Así, mi hipótesis era que cuanto mayor fuera su radio, la imprecisión de utilizar puntos en una pantalla se diluiría, y se aproximaría poco a poco, convergiendo hacia el valor de PI.

Arriba se pueden ver dos círculos en una malla de 8x8 puntos. Incluso se puede apreciar en un ejemplo tan limitado que, cuanto más se aumenta el radio, más se "parece" a un círculo real.

Hardware y software

El navegador empleado fue Falkon v24.12.3, en una máquina Intel Core i7-7700 con 32GB de RAM corriendo Manjaro Linux sobre un Kernel 6.13.7.

Calculando el valor de PI mediante el perímetro

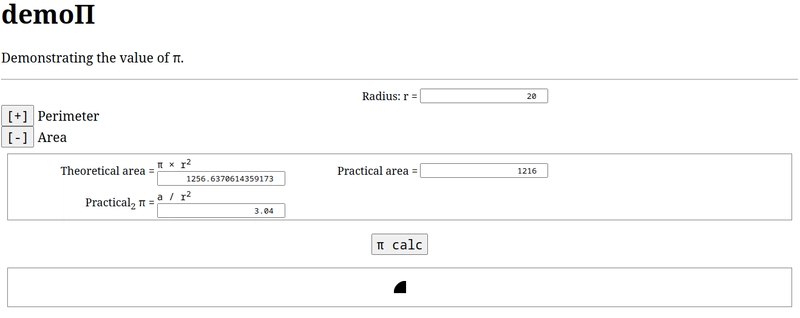
Dicho y hecho, preparé usando HTML5 un código JavaScript que calcularía el valor de PI. Exploraremos primero la parte superior, que se basa en el perímetro de un círculo.

Empezamos con un valor de radio r = 3. Parece un inicio prometedor... ¿no? La idea es que poco a poco, a medida que aumentemos el radio, vayamos obteniendo un valor que se vaya afianzando. Por ejemplo, partir de 3 y pasar por 3.2, y después por 3.15, y después... no sería necesariamente esta la secuencia exacta, pero bueno, se entiende la idea.

El programa dibuja un círculo en la parte inferior, y cuenta los puntos para el perímetro, de forma que después pueda dividirlos por el diámetro. Cambiamos el radio en la parte superior, y pulsamos Calcular PI en la parte inferior. Un cuarto de círculo se dibujará, el programa contará los puntos, y mostrará el resultado. En cuanto al resultado, a la izquierda aparece el valor de PI calculado de forma teórica (por llamarlo de alguna forma, y poder diferenciarlos), y a la derecha aparece calculado de forma práctica, es decir, contando los puntos como ya hemos explicado.

Obtuve la siguiente tabla.

Radio	Valor de PI
20	3
25	2.88
30	2.93
35	2.85

Mi gozo en un pozo. No estaba funcionando. El valor bajaba, y después subía. Seguí intentándolo con valores mucho más grandes, a ver si era cuestión de precisión.

Radio	Valor de PI
235	2.84
470	2.83
1470	2.83
6470	2.82

Quizás lo que se podía concluir era que el supuesto valor de PI iba descendiendo, centrándose en cifras claramente erróneas. Este método no funcionaba.

Calculando el valor de PI mediante el área

La ecuación para el perímetro de la circunferencia no es la única que involucra a PI: la del área a del círculo con radio r también lo hace: a = PI r².

Si desarrollamos este resultado para poder encontrar el valor de PI, obtenemos que:

a = PI r²
PI = a / r²

Volvemos al método de dibujar el círculo y contar sus puntos; solo que esta vez, en lugar de contar los puntos de la circunferencia del círculo, contamos los puntos del interior del círculo. Dado que estamos pintando el círculo en negro sobre blanco, solo es necesario contar los puntos de color negro.

Ahora desplegamos los campos dedicados al cálculo del Área pulsando en su botón [+], y descartamos la vista del perímetro pulsando en su botón [-].

Para un radio r = 20, el valor calculado de PI es 3.04. También nos indica cuál es el número de puntos relativos al área, que resulta ser 1216.

Si alimentamos el programa con valores de radio cada vez más altos, lo que esperamos es que el valor de PI calculado mediante el conteo de puntos cada vez se aproxime más a 3, después a 3.1, después a 3.14 (¿o 3.12?).

En la siguiente tabla aparecen los intentos que hice.

Radio	Valor de PI
20	3.04
25	3.04
30	3.05
35	3.06

¡Esto pinta mucho mejor! Vamos a probar con valores más altos...

Radio	Valor de PI
100	3.12
150	3.12
200	3.13
250	3.13

De acuerdo, pero todavía no tenemos la precisión necesaria. Veamos...

Radio	Valor de PI
1000	3.14
1500	3.14
2000	3.14
2500	3.14

¡Esto es bueno! Los decimales van creciendo, pero en ningún caso pasamos de 3.14. Es muy buena noticia.

Radio	Valor de PI
10000	3.1412
15000	3.1413
16000	3.1414
17000	??

...y aquí nos topamos con un problema. A pesar de dibujar tan solo un cuarto del círculo (multiplicando por cuatro los puntos encontrados para el área), resulta que con 17000 puntos de radio ya excedemos la capacidad de memoria reservada por el navegador para el canvas.

Conclusiones

Está claro que el método presentado aquí es un poco primitivo, pero por lo menos nos permite llegar a asegurar que PI está más cerca de 3.1416 que, desde luego, de 3.12.