Big-O en Español - Parte 4

Este es el último post de la serie sobre la notación Big-O. En este artículo, analizaremos el rendimiento de cada tipo de expresión y aprenderemos cómo combinar diferentes complejidades en un algoritmo. ¿Qué encontrarás en esta serie? Parte 1: Expresiones Lineales y Constantes Introducción a las notaciones más simples y cómo afectan el rendimiento de nuestros algoritmos. Parte 2: Expresiones Cuadráticas, Cúbicas y de Otras Potencias Un análisis más profundo sobre cómo crecen los tiempos de ejecución en algoritmos más complejos. Parte 3: Expresiones Logarítmicas, Exponenciales y Factoriales Exploraremos casos donde el tiempo de ejecución crece de forma mucho más drástica. Parte 4: Combinando Complejidades y Comparando Estructuras de Datos Analizaremos cómo diferentes estructuras de datos afectan la complejidad y cómo combinar varios algoritmos. Parte 5: Consideraciones Avanzadas y Casos Reales Reflexiones finales sobre trade-offs entre tiempo y espacio, complejidades amortizadas, y cómo aplicar Big-O en escenarios reales. Gráfico de Complejidad de Big-O Referencia: Big-O Cheat Sheet Como vimos en los posts anteriores, las expresiones constantes (O(1)) y logarítmicas (O(Log n)) son las de mejor rendimiento, mientras que las exponenciales (O(2^n)) y factoriales (O(n!)) son las menos eficientes. Complejidad de Algoritmos con Números La siguiente tabla ilustra cómo aumenta el tiempo de procesamiento a medida que crece el número de elementos: Notación Big-O 10 elementos 100 elementos 1000 elementos O(1) 1 1 1 O(n) 10 100 1000 O(Log n) 1 2 3 O(n²) 100 10,000 1,000,000 O(2^n) 1024 1.27e+30 1.07e+301 O(n!) 3,628,800 9.33e+157 Infinito Nota: Estos valores no representan tiempos en segundos. Gracias a los procesadores modernos, incluso los algoritmos mal diseñados pueden ejecutarse en milisegundos para volúmenes de datos pequeños. Sin embargo, es crucial entender cómo el crecimiento exponencial o factorial puede impactar significativamente nuestros sistemas cuando los datos aumentan. Operaciones Según el Tipo de Estructura de Datos La siguiente tabla muestra la notación Big-O asociada a diferentes estructuras de datos: Referencia: Big-O Cheat Sheet Comparación de Arreglo, Pila (Stack) y Cola (Queue) Acceso: Los arreglos tienen mejor rendimiento en acceso aleatorio (O(1)) en comparación con pilas y colas. Inserción y Eliminación: Las pilas y colas son más eficientes (O(1)) para estas operaciones. Búsqueda: Para los tres casos, la búsqueda tiene una complejidad lineal (O(n)). Es esencial comprender estas diferencias para tomar decisiones informadas al seleccionar estructuras de datos. ¿Qué Pasa Cuando un Código Tiene Múltiples Complejidades? Si un algoritmo combina diferentes complejidades, siempre se considera la mayor al evaluar el rendimiento general. Por ejemplo: O(1) O(n) O(n²) O = O(1) + O(n) + O(n²) = O(n²) En términos matemáticos: f(x) = 1 + x + x² Gráfica La gráfica de esta función muestra cómo domina la complejidad cuadrática en comparación con las otras: Conclusión Con este artículo, cerramos la serie sobre Big-O. Ahora tienes una visión integral de cómo analizar y optimizar algoritmos basándote en su complejidad computacional. ¡Gracias por leer! Si te gustó esta serie, no dudes en compartirla con otros desarrolladores interesados en mejorar su comprensión de algoritmos.

Mar 18, 2025 - 19:41

Este es el último post de la serie sobre la notación Big-O. En este artículo, analizaremos el rendimiento de cada tipo de expresión y aprenderemos cómo combinar diferentes complejidades en un algoritmo.

¿Qué encontrarás en esta serie?

Parte 1: Expresiones Lineales y Constantes

Introducción a las notaciones más simples y cómo afectan el rendimiento de nuestros algoritmos.
Parte 2: Expresiones Cuadráticas, Cúbicas y de Otras Potencias

Un análisis más profundo sobre cómo crecen los tiempos de ejecución en algoritmos más complejos.
Parte 3: Expresiones Logarítmicas, Exponenciales y Factoriales

Exploraremos casos donde el tiempo de ejecución crece de forma mucho más drástica.
Parte 4: Combinando Complejidades y Comparando Estructuras de Datos

Analizaremos cómo diferentes estructuras de datos afectan la complejidad y cómo combinar varios algoritmos.
Parte 5: Consideraciones Avanzadas y Casos Reales

Reflexiones finales sobre trade-offs entre tiempo y espacio, complejidades amortizadas, y cómo aplicar Big-O en escenarios reales.

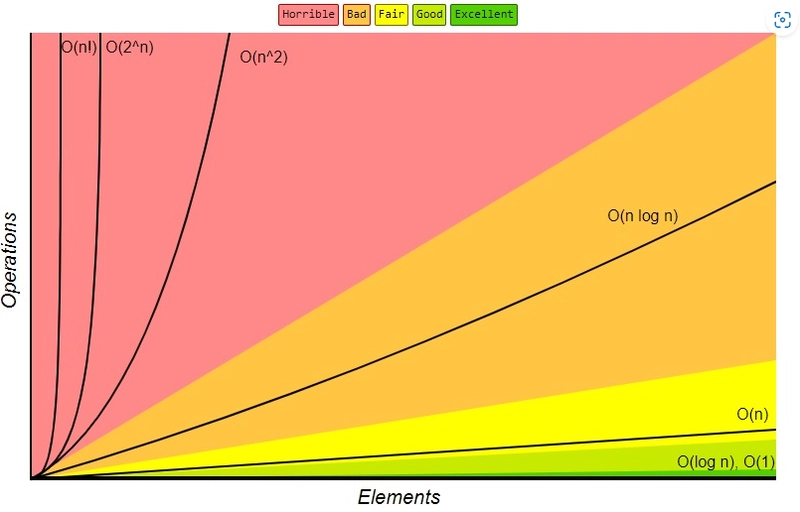
Gráfico de Complejidad de Big-O

Referencia: Big-O Cheat Sheet

Como vimos en los posts anteriores, las expresiones constantes (O(1)) y logarítmicas (O(Log n)) son las de mejor rendimiento, mientras que las exponenciales (O(2^n)) y factoriales (O(n!)) son las menos eficientes.

Complejidad de Algoritmos con Números

La siguiente tabla ilustra cómo aumenta el tiempo de procesamiento a medida que crece el número de elementos:

Notación Big-O	10 elementos	100 elementos	1000 elementos
O(1)	1	1	1
O(n)	10	100	1000
O(Log n)	1	2	3
O(n²)	100	10,000	1,000,000
O(2^n)	1024	1.27e+30	1.07e+301
O(n!)	3,628,800	9.33e+157	Infinito

Nota: Estos valores no representan tiempos en segundos. Gracias a los procesadores modernos, incluso los algoritmos mal diseñados pueden ejecutarse en milisegundos para volúmenes de datos pequeños. Sin embargo, es crucial entender cómo el crecimiento exponencial o factorial puede impactar significativamente nuestros sistemas cuando los datos aumentan.

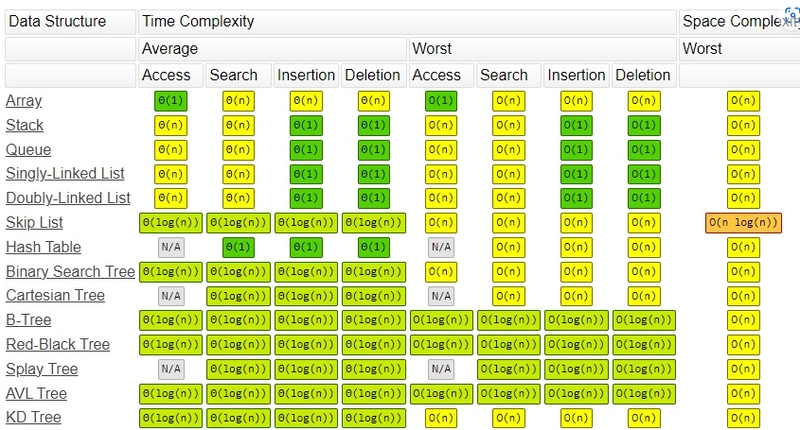
Operaciones Según el Tipo de Estructura de Datos

La siguiente tabla muestra la notación Big-O asociada a diferentes estructuras de datos:

Referencia: Big-O Cheat Sheet

Comparación de Arreglo, Pila (Stack) y Cola (Queue)

Acceso: Los arreglos tienen mejor rendimiento en acceso aleatorio (O(1)) en comparación con pilas y colas.
Inserción y Eliminación: Las pilas y colas son más eficientes (O(1)) para estas operaciones.
Búsqueda: Para los tres casos, la búsqueda tiene una complejidad lineal (O(n)).

Es esencial comprender estas diferencias para tomar decisiones informadas al seleccionar estructuras de datos.

¿Qué Pasa Cuando un Código Tiene Múltiples Complejidades?

Si un algoritmo combina diferentes complejidades, siempre se considera la mayor al evaluar el rendimiento general.

Por ejemplo:

O(1) 
O(n) 
O(n²)

O = O(1) + O(n) + O(n²) = O(n²)

En términos matemáticos:

f(x) = 1 + x + x²

Gráfica

La gráfica de esta función muestra cómo domina la complejidad cuadrática en comparación con las otras:

Conclusión

Con este artículo, cerramos la serie sobre Big-O. Ahora tienes una visión integral de cómo analizar y optimizar algoritmos basándote en su complejidad computacional.

¡Gracias por leer! Si te gustó esta serie, no dudes en compartirla con otros desarrolladores interesados en mejorar su comprensión de algoritmos.