2843. Count Symmetric Integers

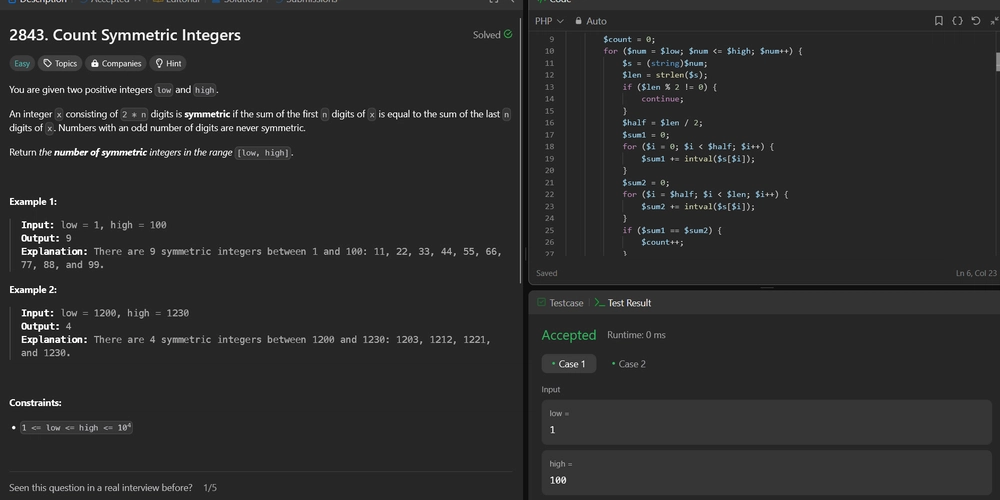
2843. Count Symmetric Integers Difficulty: Easy Topics: Math, Enumeration You are given two positive integers low and high. An integer x consisting of 2 * n digits is symmetric if the sum of the first n digits of x is equal to the sum of the last n digits of x. Numbers with an odd number of digits are never symmetric. Return the number of symmetric integers in the range [low, high]. Example 1: Input: low = 1, high = 100 Output: 9 Explanation: There are 9 symmetric integers between 1 and 100: 11, 22, 33, 44, 55, 66, 77, 88, and 99. Example 2: Input: low = 1200, high = 1230 Output: 4 Explanation: There are 4 symmetric integers between 1200 and 1230: 1203, 1212, 1221, and 1230. Constraints: 1

Apr 11, 2025 - 15:57

Difficulty: Easy

Topics: Math, Enumeration

You are given two positive integers low and high.

An integer x consisting of 2 * n digits is symmetric if the sum of the first n digits of x is equal to the sum of the last n digits of x. Numbers with an odd number of digits are never symmetric.

Return the number of symmetric integers in the range [low, high].

Example 1:

Input: low = 1, high = 100
Output: 9
Explanation: There are 9 symmetric integers between 1 and 100: 11, 22, 33, 44, 55, 66, 77, 88, and 99.

Example 2:

Input: low = 1200, high = 1230
Output: 4
Explanation: There are 4 symmetric integers between 1200 and 1230: 1203, 1212, 1221, and 1230.

Constraints:

1 <= low <= high <= 10⁴

Hint:

Iterate over all numbers from low to high
Convert each number to a string and compare the sum of the first half with that of the second.

Solution:

We need to count the number of symmetric integers within a given range [low, high]. A symmetric integer is defined as a number with an even number of digits where the sum of the first half of the digits is equal to the sum of the second half of the digits.

Approach

Iterate through the range: Check each number from low to high inclusive.
Check for even digit count: Convert each number to a string to determine its length. If the length is odd, the number cannot be symmetric, so we skip it.
Split and sum digits: For numbers with even digits, split the digits into two halves. Calculate the sum of the digits in the first half and the sum of the digits in the second half.
Compare sums: If the sums of the two halves are equal, the number is symmetric, and we increment our count.

Let's implement this solution in PHP: 2843. Count Symmetric Integers


/**
 * @param Integer $low
 * @param Integer $high
 * @return Integer
 */
function countSymmetricIntegers($low, $high) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example usage:
echo countSymmetricIntegers(1, 100); // Output: 9
echo "\n";
echo countSymmetricIntegers(1200, 1230); // Output: 4
?>

Explanation:

Iteration through the range: The loop runs from low to high, checking each number in the range.
Digit count check: Converting each number to a string allows us to check its length. If the length is odd, we skip further checks for that number.
Splitting and summing digits: For numbers with even digits, we split the string into two halves. We then sum the digits of each half separately.
Comparison of sums: If the sums of the two halves are equal, the number is counted as symmetric.

This approach efficiently checks each number in the range and ensures we only consider valid symmetric integers, providing the correct count with a time complexity of O(N * M), where N is the range size and M is the average number of digits, which is manageable given the problem constraints.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks