2560. House Robber IV

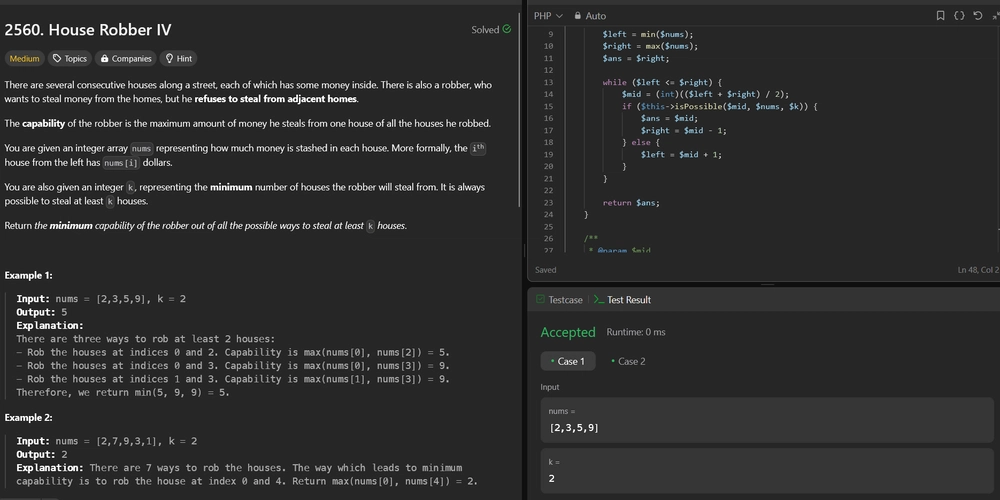
2560. House Robber IV Difficulty: Medium Topics: Array, Binary Search There are several consecutive houses along a street, each of which has some money inside. There is also a robber, who wants to steal money from the homes, but he refuses to steal from adjacent homes. The capability of the robber is the maximum amount of money he steals from one house of all the houses he robbed. You are given an integer array nums representing how much money is stashed in each house. More formally, the ith house from the left has nums[i] dollars. You are also given an integer k, representing the minimum number of houses the robber will steal from. It is always possible to steal at least k houses. Return the minimum capability of the robber out of all the possible ways to steal at least k houses. Example 1: Input: nums = [2,3,5,9], k = 2 Output: 5 Explanation: There are three ways to rob at least 2 houses: Rob the houses at indices 0 and 2. Capability is max(nums[0], nums[2]) = 5. Rob the houses at indices 0 and 3. Capability is max(nums[0], nums[3]) = 9. Rob the houses at indices 1 and 3. Capability is max(nums[1], nums[3]) = 9. Therefore, we return min(5, 9, 9) = 5. Example 2: Input: nums = [2,7,9,3,1], k = 2 Output: 2 Explanation: There are 7 ways to rob the houses. The way which leads to minimum capability is to rob the house at index 0 and 4. Return max(nums[0], nums[4]) = 2. Constraints: 1

Mar 15, 2025 - 19:04

Difficulty: Medium

Topics: Array, Binary Search

There are several consecutive houses along a street, each of which has some money inside. There is also a robber, who wants to steal money from the homes, but he refuses to steal from adjacent homes.

The capability of the robber is the maximum amount of money he steals from one house of all the houses he robbed.

You are given an integer array nums representing how much money is stashed in each house. More formally, the i^th house from the left has nums[i] dollars.

You are also given an integer k, representing the minimum number of houses the robber will steal from. It is always possible to steal at least k houses.

Return the minimum capability of the robber out of all the possible ways to steal at least k houses.

Example 1:

Input: nums = [2,3,5,9], k = 2
Output: 5
Explanation: There are three ways to rob at least 2 houses:
- Rob the houses at indices 0 and 2. Capability is max(nums[0], nums[2]) = 5.
- Rob the houses at indices 0 and 3. Capability is max(nums[0], nums[3]) = 9.
- Rob the houses at indices 1 and 3. Capability is max(nums[1], nums[3]) = 9. Therefore, we return min(5, 9, 9) = 5.

Example 2:

Input: nums = [2,7,9,3,1], k = 2
Output: 2
Explanation: There are 7 ways to rob the houses. The way which leads to minimum capability is to rob the house at index 0 and 4. Return max(nums[0], nums[4]) = 2.

Constraints:

1 <= nums.length <= 10⁵
1 <= nums[i] <= 10⁹
1 <= k <= (nums.length + 1)/2

Hint:

Can we use binary search to find the minimum value of a non-contiguous subsequence of a given size k?
Initialize the search range with the minimum and maximum elements of the input array.
Use a check function to determine if it is possible to select k non-consecutive elements that are less than or equal to the current "guess" value.
Adjust the search range based on the outcome of the check function, until the range converges and the minimum value is found.

Solution:

We need to determine the minimum capability of a robber who steals from at least k non-consecutive houses, where the capability is defined as the maximum amount stolen from any single house. The solution involves using binary search to efficiently find the minimum possible capability.

Approach

Binary Search: We use binary search to narrow down the possible values for the robber's capability. The search range is between the minimum and maximum values in the given array.
Check Function: For each midpoint value during the binary search, we check if it's possible to steal from at least k non-consecutive houses where each stolen amount is less than or equal to the midpoint value. This check is done using a greedy approach to maximize the number of non-consecutive houses the robber can steal from.

Let's implement this solution in PHP: 2560. House Robber IV


/**
 * @param Integer[] $nums
 * @param Integer $k
 * @return Integer
 */
function minCapability($nums, $k) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

/**
 * @param $mid
 * @param $nums
 * @param $k
 * @return bool
 */
function isPossible($mid, $nums, $k) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example test cases
echo minCapability([2, 3, 5, 9], 2) . "\n"; // Output: 5
echo minCapability([2, 7, 9, 3, 1], 2) . "\n"; // Output: 2
?>

Explanation:

Binary Search Initialization: The binary search is initialized with left as the minimum value in the array and right as the maximum value. This sets the initial search range for the capability.
Midpoint Check: For each midpoint value, we use the isPossible function to check if at least k non-consecutive houses can be stolen from with each house's value not exceeding the midpoint.
Greedy Check Function: The isPossible function iterates through the array, counting how many non-consecutive houses can be stolen from without exceeding the current midpoint value. This is done using a greedy approach where we always take the earliest possible valid house to maximize the count.
Adjust Search Range: Based on the result of the isPossible function, the binary search adjusts its range. If stealing from at least k houses is possible, the upper bound is decreased to seek a smaller capability. Otherwise, the lower bound is increased.

This approach efficiently narrows down the minimum capability using binary search combined with a linear-time check, ensuring optimal performance even for large input sizes.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks